Ио́ганн Ке́плер (нем. Johannes Kepler; 27 декабря 1571 года, Вайль-дер-Штадт — 15 ноября 1630 года, Регенсбург) — немецкий математик, астроном, механик, оптик, первооткрыватель законов движения планет Солнечной системы.

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце. Форма эллипса и степень его сходства с окружностью характеризуется отношением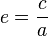 , где
, где  — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),
— расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),  — большая полуось. Величина
— большая полуось. Величина  называется эксцентриситетом эллипса. При
называется эксцентриситетом эллипса. При  , и, следовательно,
, и, следовательно,  эллипс превращается в окружность.
эллипс превращается в окружность.

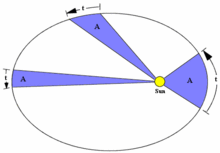
Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.
 , где
, где  и
и  — периоды обращения двух планет вокруг Солнца, а
— периоды обращения двух планет вокруг Солнца, а  и
и 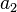 — длины больших полуосей их орбит.
— длины больших полуосей их орбит.
В конце XVI века в астрономии ещё происходила борьба между геоцентрической системой Птолемея и гелиоцентрической системой Коперника. Противники системы Коперника ссылались на то, что в отношении погрешности расчётов она ничем не лучше птолемеевской. Напомним, что в модели Коперника планеты равномерно движутся по круговым орбитам: чтобы согласовать это предположение с видимой неравномерностью движения планет, Копернику пришлось ввести дополнительные движения по эпициклам. Хотя эпициклов у Коперника было меньше, чем у Птолемея, его астрономические таблицы, первоначально более точные, чем птолемеевы, вскоре существенно разошлись с наблюдениями, что немало озадачило и охладило восторженных коперниканцев.
Открытые Кеплером три закона движения планет полностью и с превосходной точностью объяснили видимую неравномерность этих движений. Вместо многочисленных надуманных эпициклов модель Кеплера включает только одну кривую — эллипс. Второй закон установил, как меняется скорость планеты при удалении или приближении к Солнцу, а третий позволяет рассчитать эту скорость и период обращения вокруг Солнца.
Хотя исторически кеплеровская система мира основана на модели Коперника, фактически у них очень мало общего (только суточное вращение Земли). Исчезли круговые движения сфер, несущих на себе планеты, появилось понятие планетной орбиты. В системе Коперника Земля всё ещё занимала несколько особое положение, поскольку центром мира Коперник объявил центр земной орбиты. У Кеплера Земля — рядовая планета, движение которой подчинено общим трём законам. Все орбиты небесных тел — эллипсы (движение по гиперболической траектории открыл позднее Ньютон), общим фокусом орбит является Солнце.
Кеплер вывел также «уравнение Кеплера», используемое в астрономии для определения положения небесных тел.
Законы планетной кинематики, открытые Кеплером, послужили позже Ньютону основой для создания теории тяготения. Ньютон математически доказал, что все законы Кеплера являются прямыми следствиями закона тяготения.
Взгляды Кеплера на устройство Вселенной за пределами Солнечной системы вытекали из его мистической философии. Солнце он полагал неподвижным, а сферу звёзд считал границей мира. В бесконечность Вселенной Кеплер не верил и в качестве аргумента предложил (1610) то, что позже получило название фотометрический парадокс: если число звёзд бесконечно, то в любом направлении взгляд наткнулся бы на звезду, и на небе не существовало бы тёмных участков.
Строго говоря, система мира Кеплера претендовала не только на выявление законов движения планет, но и на гораздо большее. Аналогично пифагорейцам, Кеплер считал мир реализацией некоторой числовой гармонии, одновременно геометрической и музыкальной; раскрытие структуры этой гармонии дало бы ответы на самые глубокие вопросы:
Я выяснил, что все небесные движения, как в их целом, так и во всех отдельных случаях, проникнуты общей гармонией — правда, не той, которую я предполагал, но ещё более совершенной.
Например, Кеплер объясняет, почему планет именно шесть (к тому времени были известны только шесть планет Солнечной системы) и они размещены в пространстве так, а не как-либо иначе: оказывается, орбиты планет вписаны в правильныемногогранники. Интересно, что исходя из этих ненаучных соображений, Кеплер предсказал существование двух спутников Марса и промежуточной планеты между Марсом и Юпитером.
Законы Кеплера соединяли в себе ясность, простоту и вычислительную мощь, однако мистическая форма его системы мира основательно засоряла реальную суть великих открытий Кеплера. Тем не менее уже современники Кеплера убедились в точности новых законов, хотя их глубинный смысл до Ньютона оставался непонятным. Никаких попыток реанимировать модель Птолемея или предложить иную систему движения, кроме гелиоцентрической, больше не предпринималось.
Кеплер немало сделал для принятия протестантами григорианского календаря (на сейме в Регенсбурге, 1613, и в Ахене, 1615).
Кеплер стал автором первого обширного (в трёх томах) изложения коперниканской астрономии (Epitome Astronomiae Copernicanae, 1617—1622), которое немедленно удостоилось чести попасть в «Индекс запрещённых книг». В эту книгу, свой главный труд, Кеплер включил описание всех своих открытий в астрономии.
Летом 1627 года Кеплер после 22 лет трудов опубликовал (за свой счёт) астрономические таблицы, которые в честь императора назвал «Рудольфовыми». Спрос на них был огромен, так как все прежние таблицы давно разошлись с наблюдениями. Немаловажно, что труд впервые включал удобные для расчётов таблицы логарифмов. Кеплеровы таблицы служили астрономам и морякам вплоть до начала XIX века.
Через год после смерти Кеплера Гассенди наблюдал предсказанное им прохождение Меркурия по диску Солнца. В 1665 году итальянский физик и астроном Джованни Альфонсо Борелли опубликовал книгу, где законы Кеплера подтверждаются для открытых Галилеем спутников Юпитера.
Первый закон Кеплера (закон эллипсов)

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце. Форма эллипса и степень его сходства с окружностью характеризуется отношением
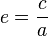 , где
, где  — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),
— расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),  — большая полуось. Величина
— большая полуось. Величина  называется эксцентриситетом эллипса. При
называется эксцентриситетом эллипса. При  , и, следовательно,
, и, следовательно,  эллипс превращается в окружность.
эллипс превращается в окружность.Второй закон Кеплера (закон площадей)

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.
Третий закон Кеплера (гармонический закон)
Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников. , где
, где  и
и  — периоды обращения двух планет вокруг Солнца, а
— периоды обращения двух планет вокруг Солнца, а  и
и 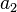 — длины больших полуосей их орбит.
— длины больших полуосей их орбит.

Комментариев нет:
Отправить комментарий