Эта статья посвящена вспомогательному инструменту для умножения, брускам, предложенным в 1885 г. железнодорожным инженером Женойем и сотрудником парижского Музея искусств и ремесел Эдуардом Люка.
Бруски Женайла и Люкаса были более удобны, чем предшествовавшие им палочки Непера, и вполне могли конкурировать с современными им брусками Иоффе (построенными на теореме Слонимского).
Информации об этом изделии в рунете практически нет. На днях я внезапно нагуглил статью на немецком языке, помогшую мне врубиться в принцип действия брусков. Не ограничиваясь статьёй, я восстановил вид рабочей поверхности брусков по картинкам с видом части из них и ориентируясь на принцип их действия. Найденные позже на том же сайте материалы подтвердили правильность моей реконструкции.
http://geektimes.ru/post/251958/
Бруски Женайла и Люкаса, как и другие подобные изделия, предназначены для быстрого получения произведения многоразрядного числа на одноразрядное.
Множительный инструмент представляет собой набор из 11 брусков. На каждом бруске нанесена цифровая шкала, по которой находится результат. Шкала разделена на 8 частей, соответствующих умножению на числа от 2 до 9. Один брусок служит подсказкой — части его шкалы подписаны цифрами 2...9 — это значения одноразрядного множителя, а сама его шкала предназначена для считывания старшего разряда произведения. Остальные бруски пронумерованы цифрами от 0 до 9 и предназначены для умножения соответствующих цифр. В них рядом со шкалой находится треугольник, правая сторона которого ограничивает слева цифровую шкалу, а левая вершина находится на левом ребре бруска — когда бруски сложены вместе, она указывает позицию следующего разряда произведения на следующем бруске.











Небольшой анализ: легко видеть, что каждая часть шкалы каждого бруска начинается с цифры равной значению разряда единиц произведения номера бруска на номер части шкалы. Например, на бруске 8 фрагмент 9 начинается с цифры 2 (8*9=72). Длина каждой части шкалы равна величине одноразрядного множителя — что естественно, т.к. при умножении любого числа на одноразрядный множитель старший разряд произведения меньше этого множителя, т.е. при умножении, например, на 5, величина переносимого в следующий разряд значения никогда не превысит 4, при умножении на 9, соответственно, 8, и т.п. Величина смещения цифры вниз от начала шкалы равно значению переноса из младшего разряда. Получается, что позиция левой вершины чёрного треугольника соответствует значению второго разряда произведения номера бруска на одноразрядный множитель, к которому прибавлено число, перенесённое из младшего разряда.
Для того, чтобы умножить многоразрядное число на одноразрядное, нужно сложить вместе бруски, с номерами, соответствующими разрядам цифр и приложить к ним слева брусок с подсказкой. Тогда в каждой части шкалы можно будет считать произведения этого числа на соответствующее одноразрядное число. Разряд единиц — это первая цифра нужной части шкалы, а каждый следующий разряд нам укажет левая вершина треугольника, правая сторона которого служит левой границей ячейки предыдущего разряда.
Например, возьмём число 7519. Сложим вместе брусок с подсказкой и бруски 7, 5, 1 и 9. Схема показана на картинке ниже.
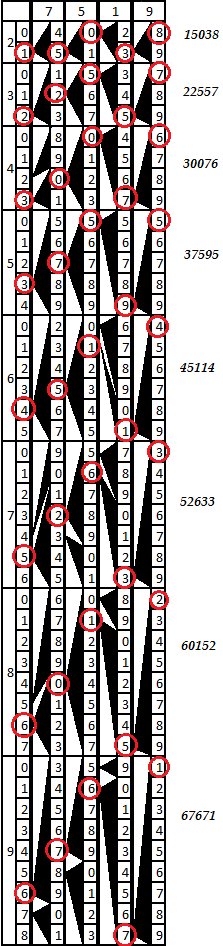
В каждой части полученной таблицы, следуя указателям-треугольникам, можно проследить справа налево разряды произведений.
Схема понятнее любых слов. Проследим, например, умножение на 9. В начале девятой (последней) части шкалы правого бруска видим цифру 1. Треугольник от неё указывает на цифру 7 соседнего бруска, оттуда треугольник указывает на 6, дальше — на 7, а ещё дальше — на цифру 6 на шкале бруска-подсказки. Т.о. получаем значение 67671 = 7519*9.
Аналогично прослеживаются другие произведения. Легко убедиться, что они верны. Следовательно, инструмент пригоден для применения.
Апокин И.А., Майстров Л.Е. в источнике [1] пишут, что у цифровых брусков были рабочими все четыре поверхности. Логично предположить, что поверхности использовались для дублирования шкал, что необходимо для составления многоразрядных чисел с несколькими вхождениями одной и той же цифры.
Исходя из количества сторон бруска, предположим, что на 10 брусках было четыре полных комплекта шкал.
Допустим, что шкалы на брусках надо расположить таким образом, чтобы бруски позволяли составить любое четырёхразрядное число.
Можно найти множество вариантов размещения рабочих шкал на брусках, удовлетворяющих этому требованию. Например, взять по два бруска пяти видов, имеющие грани, соответственно:
0,1,2,3;
2,3,4,5;
4,5,6,7;
6,7,8,9;
0,1,8,9.
Другой вариант использования четырёх граней — расположить на них по частям одну шкалу и уменьшить таким образом длину бруска. Этот вариант менее удобен для использования, т.к. не позволяет видеть сразу все произведения.
Шкала состоит из 8 частей, имеющих длину от 2 до 9. Собрать их в четыре группы без нарушения порядка можно так:
2+3+4+5=14; 6+7=13; 8; 9. Наибольшая длина — 14.
Если допустимо нарушить порядок, то части шкалы легко группируются:
2+9; 3+8; 4+7; 6+5. Т.е. длина бруска сокращается до 11.
1. Апокин И.А., Майстров Л.Е. «История вычислительной техники: От простейших счетных приспособлений до сложных релейных систем.» (Москва: Издательство «Наука», 1990)
2. www.mechrech.info
Бруски Женайла и Люкаса были более удобны, чем предшествовавшие им палочки Непера, и вполне могли конкурировать с современными им брусками Иоффе (построенными на теореме Слонимского).
Информации об этом изделии в рунете практически нет. На днях я внезапно нагуглил статью на немецком языке, помогшую мне врубиться в принцип действия брусков. Не ограничиваясь статьёй, я восстановил вид рабочей поверхности брусков по картинкам с видом части из них и ориентируясь на принцип их действия. Найденные позже на том же сайте материалы подтвердили правильность моей реконструкции.
http://geektimes.ru/post/251958/
Бруски Женайла и Люкаса, как и другие подобные изделия, предназначены для быстрого получения произведения многоразрядного числа на одноразрядное.
Множительный инструмент представляет собой набор из 11 брусков. На каждом бруске нанесена цифровая шкала, по которой находится результат. Шкала разделена на 8 частей, соответствующих умножению на числа от 2 до 9. Один брусок служит подсказкой — части его шкалы подписаны цифрами 2...9 — это значения одноразрядного множителя, а сама его шкала предназначена для считывания старшего разряда произведения. Остальные бруски пронумерованы цифрами от 0 до 9 и предназначены для умножения соответствующих цифр. В них рядом со шкалой находится треугольник, правая сторона которого ограничивает слева цифровую шкалу, а левая вершина находится на левом ребре бруска — когда бруски сложены вместе, она указывает позицию следующего разряда произведения на следующем бруске.











Небольшой анализ: легко видеть, что каждая часть шкалы каждого бруска начинается с цифры равной значению разряда единиц произведения номера бруска на номер части шкалы. Например, на бруске 8 фрагмент 9 начинается с цифры 2 (8*9=72). Длина каждой части шкалы равна величине одноразрядного множителя — что естественно, т.к. при умножении любого числа на одноразрядный множитель старший разряд произведения меньше этого множителя, т.е. при умножении, например, на 5, величина переносимого в следующий разряд значения никогда не превысит 4, при умножении на 9, соответственно, 8, и т.п. Величина смещения цифры вниз от начала шкалы равно значению переноса из младшего разряда. Получается, что позиция левой вершины чёрного треугольника соответствует значению второго разряда произведения номера бруска на одноразрядный множитель, к которому прибавлено число, перенесённое из младшего разряда.
Для того, чтобы умножить многоразрядное число на одноразрядное, нужно сложить вместе бруски, с номерами, соответствующими разрядам цифр и приложить к ним слева брусок с подсказкой. Тогда в каждой части шкалы можно будет считать произведения этого числа на соответствующее одноразрядное число. Разряд единиц — это первая цифра нужной части шкалы, а каждый следующий разряд нам укажет левая вершина треугольника, правая сторона которого служит левой границей ячейки предыдущего разряда.
Например, возьмём число 7519. Сложим вместе брусок с подсказкой и бруски 7, 5, 1 и 9. Схема показана на картинке ниже.

В каждой части полученной таблицы, следуя указателям-треугольникам, можно проследить справа налево разряды произведений.
Схема понятнее любых слов. Проследим, например, умножение на 9. В начале девятой (последней) части шкалы правого бруска видим цифру 1. Треугольник от неё указывает на цифру 7 соседнего бруска, оттуда треугольник указывает на 6, дальше — на 7, а ещё дальше — на цифру 6 на шкале бруска-подсказки. Т.о. получаем значение 67671 = 7519*9.
Аналогично прослеживаются другие произведения. Легко убедиться, что они верны. Следовательно, инструмент пригоден для применения.
Спекуляции на тему внешнего вида
Апокин И.А., Майстров Л.Е. в источнике [1] пишут, что у цифровых брусков были рабочими все четыре поверхности. Логично предположить, что поверхности использовались для дублирования шкал, что необходимо для составления многоразрядных чисел с несколькими вхождениями одной и той же цифры.
Исходя из количества сторон бруска, предположим, что на 10 брусках было четыре полных комплекта шкал.
Допустим, что шкалы на брусках надо расположить таким образом, чтобы бруски позволяли составить любое четырёхразрядное число.
Можно найти множество вариантов размещения рабочих шкал на брусках, удовлетворяющих этому требованию. Например, взять по два бруска пяти видов, имеющие грани, соответственно:
0,1,2,3;
2,3,4,5;
4,5,6,7;
6,7,8,9;
0,1,8,9.
Другой вариант использования четырёх граней — расположить на них по частям одну шкалу и уменьшить таким образом длину бруска. Этот вариант менее удобен для использования, т.к. не позволяет видеть сразу все произведения.
Шкала состоит из 8 частей, имеющих длину от 2 до 9. Собрать их в четыре группы без нарушения порядка можно так:
2+3+4+5=14; 6+7=13; 8; 9. Наибольшая длина — 14.
Если допустимо нарушить порядок, то части шкалы легко группируются:
2+9; 3+8; 4+7; 6+5. Т.е. длина бруска сокращается до 11.
Литература
1. Апокин И.А., Майстров Л.Е. «История вычислительной техники: От простейших счетных приспособлений до сложных релейных систем.» (Москва: Издательство «Наука», 1990)
2. www.mechrech.info
Комментариев нет:
Отправить комментарий