Более подробно дело происходило так: «В 1696 г. в июньской книге лейпцигского журнала «Acda Eruditorum» И. Бернулли опубликовал заметку «Problema novum ad cujus solutionem matematice invitantur». (Новая задача, к разрешению которой приглашаются математики). В этой заметке говорилось: «В вертикальной плоскости даны две точки А и В. Определить путь АМВ, спускаясь по которому под влиянием собственной тяжести тело М, начав двигаться из точки А дойдёт до другой точки В в кратчайшее время. Для того чтобы вызвать интерес со стороны любителей подобных вопросов и побудить их охотнее предпринять попытку разрешения указанной задачи, довожу до их сведения, что эта задача не сводится к пустой умственной спекуляции, лишённой какого бы то ни было практического значения, как это может кому-либо показаться. В действительности она представляет большой практический интерес, и притом, кроме механики, также и для других дисциплин, что может всем показаться неправдоподобным».
Это была знаменитая задача о брахистохроне, или кривой наискорейшего ската: даны две точки в вертикальной плоскости, не лежащие на одной вертикали; найти вид кривой линии, спускаясь по которой тяжелое тело прошло бы путь между этими точками в наименьшее время. Решение этой, по словам Лейбница, «столь прекрасной и до сих пор неслыханной задачи» было дано самим И. Бернулли, Лейбницем, Ньютоном, Я. Бернулли и Лопиталем. На решение предложенной задачи И. Бернулли дал полугодичный срок, но за это время решение прислал только Лейбниц. Поэтому по его предложению И. Бернулли продлил срок до пасхи 1697 г.
В этот срок задача была решена также Ньютоном, Якобом Бернулли и Лопиталем, которые нашли, что кривой наибыстрейшего спуска является циклоида. Решение Ньютона было напечатано в майском номере «Philosophical Transactions» за 1697 г. (N 224, с. 384) без подписи автора. В майском же номере «Ada Eruditorum» за 1697 г.. в котором опубликовал своё решение И. Бернулли, была напечатана статья его старшего брата Я. Бернулли и статья Лопиталя с аналогичными решениями. В решении И. Бернулли речь идёт одновременно об оптике и механике, о движении луча и тяжелой частицы. Указав на то, что Ферма вывел закон преломления света из принципа кратчайшего времени (при V = const принцип кратчайшего времени Ферма переходит в принцип кратчайшего пути), И. Бернулли рассматривает задачу о кривизне луча в неоднородных прозрачных средах. Этому вопросу им посвящена работа «Кривизна луча в неоднородных прозрачных средах и решение задачи, предложенной мной в «Acta» за 1696 г., о нахождении брахистохронной линии, т.е. такой линии, по которой тело должно проходить от одной заданной точки до другой в кратчайшее время; затем о построении синхронной кривой, т.е. «волны лучей». И. Бернулли не ищет общих методов решения задачи отыскания максимума или минимума какой-либо функции, он указывает, что сомневается и в самой возможности существования таких общих методов. Его цель - дать метод решения специальной задачи, задачи о брахистохроне, метод, который может оказаться применимым и для других задач аналогичного характера.
Прежде всего Бернулли указывает на тот изумительный, по его мнению, результат, что брахистохроной, так же как и таутохроной Гюйгенса, является циклоида. Этот результат он нашел двумя путями: косвенным и прямым. Тут же И. Бернулли дает, по существу, первую формулировку оптико-механической аналогии, хотя, конечно, ещё в очень частной форме: «Я укажу, что мною открыто удивительное совпадение между кривизной луча света в непрерывно изменяющейся среде и нашей брахистохронной кривой». Воспользовавшись принципом Ферма, представляя луч в виде «шарика» и исходя из связи синусов углов падения и преломления со скоростями в среде данной разреженности (или обратной плотности), И. Бернулли без труда приходит к выводу, что в среде, как бы разделённой бесконечно большим количеством горизонтально расположенных пластинок, промежутки между которыми заполнены прозрачной материей, плотность которой возрастает или убывает в определенном отношении, траектория светового луча будет брахистохроной. Это значит, что она такова же, что и в случае движения тяжёлых тел. «Так как, - восклицает И. Бернулли, отчётливо выражая основную идею оптико-механической аналогии, - в обоих случаях кривая подчинена тому условию, что она должна быть пройдена в кратчайшее время, то что мешает нам поставить одно на место другого?».
Полак Л.С., Уильям Гамильтон, М., «Наука», 1993 г., с. 88-90.
Пусть имеются две произвольные точки, расположенные на разных ординатах. Далее пусть произвольная материальная точка M скатывается от точки A к точке B под действием только силы тяжести (силы трения отсутствуют). Найдем такую траекторию, при которой время скатывания будет минимально.
Направим ось ординат вниз и сопоставим начальной точке нулевое значение ординаты. Запишем закон сохранения энергии для материальной точки M:
-
, где
— масса тела,
— ускорение свободного падения,
— ордината,
— скорость движения тела.
Получаем:
-
,
откуда можно найти значение проекции скорости на ось 
:
:-
.
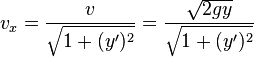Поскольку время на спуск равняется 
, то задача сводится к минимизации значения интеграла
, то задача сводится к минимизации значения интеграла-
.- Решением задачи о брахистохроне является дуга циклоиды с горизонтальным основанием, точка возврата которой находится в точке А, или иными словами, имеющая вертикальную касательную в точке A.Примечательно, что время спуска не зависит от расположения начальной точки на дуге циклоиды.
- Цикло́ида (от греч. κυκλοειδής — круглый) — плоская трансцендентная кривая. Циклоида определяется кинематически как траектория фиксированной точки производящей окружности радиуса
, катящейся без скольжения по прямой. 
Комментариев нет:
Отправить комментарий