https://geektimes.ru/post/276432/
Задача по математике 9 класс 1.1.3 (3 балла)
Локатор видит часть пространства, ограниченную конусом. Максимальный угол между образующими этого конуса равен 60 градусам. Объекты, находящиеся дальше расстояния a, уже далеко и не попадают в зону видимости локатора. Через ось конуса проведены две перпендикулярные плоскости, которые делят конус на четыре части. В одной из частей обнаружен объект в форме сферы, вписанный в эту часть. Сфера касается обеих перпендикулярных плоскостей, поверхности конуса и его основания. Длина образующей равна a. Найдите радиус этой сферы.
Задача по физике 9 класс 1.2.4 (3 балла)
В ходе эксперимента по выращиванию кристалла сломалась система охлаждения, и уже выращенный образец расплавился. Для изучения остался только график зависимости температуры от времени, но и он был поврежден. Восстановите цену делений на этом графике. Известно что теплопередача пропорциональна разнице температур, внешняя температура 400 K. Про материал известны: температура плавления 300 K, теплота плавления λ=24кКал/кг, теплоемкость жидкой фазы Сж=8000кал/кг*К, коэффициент теплопроводности 32 Дж/градус Масса образца 1 кг.

Запишите цену делений шкалы температуры. Ответ дайте в градусах, с точностью до целых.
Задача по физике 9 класс 1.2.5 (4 балла)
Спутник, находящийся на высоте H = 7000 км от центра планеты с массой M=1,076*1023 кг, переходит на точно такую же по высоте орбиту, пересекающую изначальную под углом α=5º. Найдите силу, с которой действовали маневровые двигатели спутника, если известно, что поворот занял t=30 с, а масса спутника m=50 кг. Ответ дайте в ньютонах с точностью до целых.
Задача по физике 10-11 класс 1.3.3 (2 балла)
Спутник массы m=100 кг, находящийся на орбите радиуса L=2500 км, обращаясь вокруг планеты массы M= 4,8017· 1022 кг, разгоняясь, совершает эллиптический переход на орбиту радиуса 2L=5000 км. Найдите время, требующееся на переход. Изменения скорости, производимые в апоцентре и перицентре, считать мгновенными. Ответ дайте в часах, с точностью до десятых.

Задача по физике 10-11 класс 1.3.5 (3 балла)
Ниже приведен график зависимости плотности атмосферы Юпитера от высоты.
Считая ускорение свободного падения g постоянным g=25м/с2, найдите глубину погружения, если зонд спускается с высоты H1=7∗ 104 км вниз без начальной скорости. Среднюю плотность зонда считайте равной ρ=1.49г/см3
Ответ дайте в километрах и округлите до тысяч.
Задача по информатике 1.4.3 «Полет» (6 баллов)
На высоте h метров над поверхностью планеты находится тело. В начальный момент времени его скорость равна v⃗метров в секунду. Вычислите время до момента касания телом поверхности планеты, если известно, что:
— h в начальный момент времени не превышает десяти километров, а мгновенная скорость — одного километра в секунду.
— На тело действует сила притяжения планеты. Ускорение, создаваемое этой силой, равно , и направлено к центру планеты. Здесь G — гравитационная постоянная, M — масса планеты, а R — расстояние от центра планеты до тела. Величину GM считайте равной 4× 1013, а радиус планеты — 6300000 метрам.
, и направлено к центру планеты. Здесь G — гравитационная постоянная, M — масса планеты, а R — расстояние от центра планеты до тела. Величину GM считайте равной 4× 1013, а радиус планеты — 6300000 метрам.
— Так же на тело действует сила аэродинамического сопротивления. Можете считать, что ускорение, создаваемое этой силой, равно , где ρ — плотность
, где ρ — плотность
атмосферы на заданной высоте, выражаемая формулой — мгновенная скорость тела, а
— мгновенная скорость тела, а  — модуль мгновенной скорости.
— модуль мгновенной скорости.
— При данных ограничениях смещение вдоль касательной к поверхности планеты много меньше ее радиуса планеты, поэтому кривизной планеты следует пренебречь.
Мы понимаем, что аналитически решить эту задачу сложно, поэтому примем ответ с абсолютной погрешностью 0.1 секунды. И предупреждаем, что слишком сильно менять состояние тела — не очень хорошая идея.
Формат входных данных:
В первой строке дано одно натуральное число h — высота тела в начальный момент времени, выраженная в метрах. Во второй строке даны два целых числа — координаты начальной скорости тела в метрах в секунду. Ось Oy при этом направлена в сторону, противоположную направлению силы гравитации, а ось Ox — перпендикулярна оси Oy.
— координаты начальной скорости тела в метрах в секунду. Ось Oy при этом направлена в сторону, противоположную направлению силы гравитации, а ось Ox — перпендикулярна оси Oy.
Пример ввода 1:
100
10 10
Пример ввода 2:
1
0 0
Формат выходных данных:
Выведите единственное вещественное число — время до касания телом поверхности планеты, выраженное в секундах.
Пример вывода 1:
290
105.3283038851984
Пример вывода 2:
1.6649107662192795
Задача 2.1 «Посадка на Луну» (макс. 180 баллов)
Луна — ближайший к Земле астрономический объект. Посадка корабля на Луну — это самое простое задание, с которым человечество справлялось уже не раз. Создание и запуск аппарата для исследования лунной поверхности состоит из нескольких этапов. В этой задаче мы мы рассмотрим только один, но самый интересный этап — посадку аппарата. Вам придется сконструировать собственный аппарат и составить техническое задание на его производство, дождаться результатов полета и получить телеметрию процесса посадки.
Успешно посадить аппарат с первой попытки не просто. В случае неудачи вам предстоит проанализировать данные телеметрии и изменить техническое задание для следующего запуска.
Постановка задачи
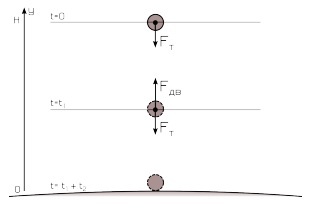
Это только первая, тренировочная задача, поэтому в ней есть несколько допущений: аппарат падает вертикально на поверхность Луны, его начальная скорость равна нулю, а из доступного оборудования есть только демпфер и тормозной двигатель.
Задача состоит в том, чтобы определить, в какой момент времени t1 нужно включить тормозной двигатель, чтобы к моменту посадки t1+t2 скорость корабля была бы меньше 50 м/с, иначе удар не удастся самортизировать с помощью демпфера.
Другими словами, вам нужно вычислить два параметра — время включения тормозного двигателя и время его выключения — и вставить их в программу полета аппарата.
Все исходные данные известны: это начальная высота, масса и радиус Луны, масса аппарата, сила тормозного двигателя.
Задача 2.2 «Посадка на Марс» (макс. 1650 баллов)
Красная Планета — намного более сложный объект для посадки космического аппарата, чем Луна. Во-первых, Марс намного массивнее, а значит сила тяжести играет куда большую роль. Во-вторых, на Марсе есть атмосфера, так что влияние сопротивления атмосферы на движение корабля около поверхности будет значительным.
В этой задаче также не будет рассматриваться работа аппарата на поверхности. В вашем распоряжении снова будет полностью сконструированный аппарат, но вам придется самостоятельно запрограммировать его полет: выбрать, в какой момент нужно будет включить тормозной двигатель, открыть парашют и т. д.
Анализ телеметрии позволит исправить ошибки, допущенные при посадке, уже в следующем аппарате.
Постановка задачи

По сравнению с Луной задача усложняется: теперь придется работать в двух измерениях. У аппарата есть начальная горизонтальная (орбитальная) скорость. К тому же, теперь на аппарат действует не только сила тяжести, но и сила аэродинамического сопротивления (Стокса), пропорциональная квадрату скорости аппарата. Однако, и в этой задаче есть упрощение: поверхность планеты принимается за плоскость. Также вам будет доступна специальная программа для расчетов.
Условие задачи делает аналитическое решение очень сложным, поэтому мы предлагаем вам качественно оценивать значения скоростей и сил, а также тщательно анализировать результаты неудачных полетов.
Задача 2.3. «Работа на поверхности Марса» (макс. 20000 баллов)
Конструирование аппарата
Мы предлагаем вам продолжить миссию по покорению Марса разработкой аппарата для работы на поверхности планеты. Совершив удачную посадку, ваш аппарат начнет передавать на Землю научные данные, которые позволят углубить знания человечества о Красной планете.
Условия победы:
За успешное решение этой миссии вы получаете победные баллы. В этой миссии вы получаете баллы за переданную на Землю научную информацию следующим образом: За каждый переданный на землю 1 Мегабит (1000 килобит) научной информации команда получает 0,1 балла (другими словами, количество баллов = переданная информация/1000). Вам дается 10 попыток. Каждая дополнительная попытка сверх этих десяти отнимает у команды 30 баллов. Таким образом можно получить не более 30 дополнительных попыток (т. е. Минус 900 баллов).В миссии также возможны следующие достижения:
Постановка задачи
Если с точки зрения физики задача остается прежней, то конструкторская ее часть будет заметно сложнее. Вам предстоит полностью сконструировать аппарат и составить программу не только посадки, но и планетарной активности. Аппарат может проработать на поверхности Марса не более 72 земных (!) часов.
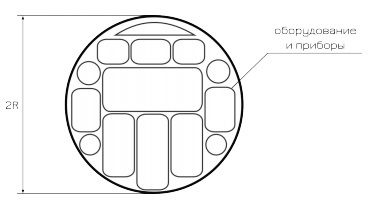
Вам не придется конструировать произвольный аппарат с нуля. В вашем распоряжении будет аппарат сферической формы, его размер вы можете установить самостоятельно. Вам придется рассчитать требуемые внешние параметры аппарата (массу и радиус), выбрать необходимое для работы оборудование и научные приборы.
Мы рекомендуем следующий порядок разработки:
Помимо конструкции аппарата вам предстоит разработать программу полета, например, определить время, когда должны включаться и выключаться тормозные двигатели или научные приборы.
Задача 2.5 «Связь с Землей» (макс. 520)
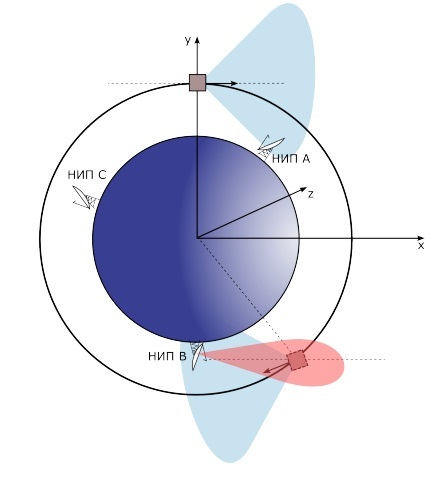
КА движется по круговой орбите с заданной высотой в плоскости X0Y. Необходимо запрограммировать аппарат так, чтобы он передал на Землю заданное сообщение. При этом необходимо воспользоваться высокопроизводительной связью КА. Задача усложняется двумя факторами: сигнал экранируется Землей, антенна такой подсистемы имеет угол раскрыва (γ), заданный в параметрах КА.
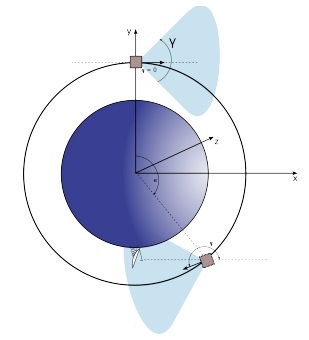
Мы будем считать, что наземный измерительный пункт (НИП) отслеживает положение КА, поэтому потребуется только сориентировать аппарат на НИП.
В данной миссии вам не потребуется конструировать аппарат целиком, однако нужно будет подобрать несколько параметров конструкции аппарата — площади солнечных батарей и радиаторов, а также написать программу полета. Мы рекомендуем вам использовать наработки, полученные в предыдущей миссии.
КА оснащен подсистемой ориентации и стабилизации, которая позволяет задавать момент вращения посредством включения маховика, а также подсистемой высокопроизводительной связи, параметры которой указаны в таблице ниже. КА как и в первой тренировочной миссии в начале полета будет иметь стартовую угловую скорость, которую придется погасить для успешного выполнения миссии.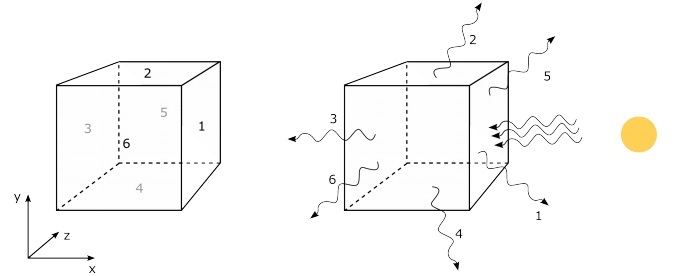
При конструировании аппарата вам необходимо рассчитать и указать площади для солнечных батарей и радиаторов на гранях 1-4 аппарата и площади радиаторов на гранях 5-6 аппарата, например:
Задача 2.7 «Съемка Земли из космоса» (макс. 12500 баллов)
Задача «Съемка Земли из космоса» посвящена съемке поверхности Земли из космоса малым космическим аппаратом. Вы должны будете сфотографировать объект на поверхности Земли и передать полученное изображение на наземный измерительный пункт (НИП), используя высокопроизводительную связь.
Задача 2.8. «SMS везде» (макс. 9200 баллов)
Задача «SMS везде» воссоздает работу спутника связи, который должен обеспечить прием и передачу сообщений между 18 наземными станциями (которые называются «0», «1», «2» и т.д.).
В вашем распоряжении будет 10 стартовых запусков. За каждый запуск после 10-го будет добавляться штраф в 150 баллов за запуск, и так до 20 дополнительных запусков (до -3000 баллов).
Постановка задачи
Каждое конструкторское бюро получает уникальный вариант, который содержит: стартовую высоту орбиты; список и названия наземных измерительных пунктов; таблицу сообщений для передачи (всего 5 сообщений).
КА должен последовательно доставить максимальное число сообщений, указанных в таблице. Как только аппарат получил сообщение от НИП, начинается отсчет времени доставки, которое не должно превысить допустимое время передачи.
На миссию дается 6 часов полета аппарата.
Задача по математике 3.1.4 (4 балла)
Магнитометр выдает для каждого градуса долготы φ три координаты вектора магнитного поля (sin φ, sin 2φ, cos 2φ). Найдите долготу, на которой вектор магнитного поля имеет минимальную длину.
Задача по физике 3.2.2 (3 балла)

Космический корабль, покоящийся в открытом космосе, вдалеке от планет представляет из себя конструкцию, изображенную на рисунке. Корабль должен был выполнить маневр ускорения, включив на короткое время τ = 2c симметрично расположенные двигатели, однако, в результате технического сбоя сработал только один из них. Каков модуль скорости, которую приобрел после этого маневра корабль в системе отсчета, в которой исходно он покоился? На какой угол повернулся корабль на момент выключения двигателя относительно оси, перпендикулярной плоскости движения, проходящей через цент основного отсека корабля?
Параметры корабля: масса корабля M = 1200кг, расстояние между центрами отсеков L = 2м, тяга двигателя F = 710Н, мощность двигателя N = 50кВт. Момент инерции корабля относительно оси, проходящей через центр масс перпендикулярно штангам равен J = 903кг·м2. Центры шаров лежат на прямой, проходящей вдоль соединяющей их штанги. Массой штанг, уменьшением массы корабля в результате сгорания топлива и гравитационным взаимодействием можно пренебрегите. Считайте, что сила тяги не зависит от скорости, а масса в отсеках распределена однородно.
Задача по физике 3.3.3 (3 балла)

Спутник облетает Землю на геостационарной орбите высотой H = 35 786 км. У спутника есть одна солнечная батарея 2м х 10м направленная всегда перпендикулярно орбите спутника длинной стороной вдоль прямой соединяющей центры Земли и спутника (см. рисунок, плоскость батареи перпендикулярна плоскости рисунка). Коэффициент отражения света от батареи β = 75% (остальной свет батареей поглощается). На какое время нужно запустить двигатель гиродина с крутящим моментом 2 Н·м, чтобы скомпенсировать вращение спутника, полученное из за солнечного излучения за время движения от положения А до положения B по орбите? Солнечная постоянная L = 1367 Вт/м², радиус орбиты Земли RЗемли = 150 млн. километров. Считайте, что коэффициент отражения не зависит от угла падения света.
Гиродин — вращающееся инерциальное устройство, применяемое для высокоточной ориентации и стабилизации.
Задача по информатике 3.4.5 «Механизм» (3 балла)
Олимпиада это, конечно, здорово и интересно, но дома у Коли осталась компьютерная игра-головоломка. На новый уровень Коля перешел буквально перед самым отъездом из дома и теперь в уме размышляет, как будет проходить новый уровень. Задача заключается в следующем: Коля собирает какой-то заумный механизм. Для этого он должен последовательно устанавливать на стержень высоты h детали механизма.
Каждая деталь представляет собой диск некоторой высоты. Все детали задаются двумя параметрами: высота детали ki и радиус детали ri. Известно, что все детали, несмотря на то, что имеют разный вид, вносят равный вклад в мощность механизма. Коля же должен сделать самый мощный механизм из возможных. При сборке механизма действуют следующие правила Детали укладываются на стержень последовательно. Радиус детали, которая лежит выше, должен быть строго меньше радиуса любой детали, которая лежит ниже.
Суммарная высота всех деталей должна быть строго меньше высоты стержня.
Помогите Коле написать программу, которая сможет выдать план сборки самого мощного механизм.
Формат входных данных:
В первой строке задано число деталей 1≤N≤5000 и высота стержня h≤20000. В следующих N строках записаны тройки целых неотрицательных чисел idi — номер детали, 0≤ki≤1000 — высота i-ой детали и 1≤ri≤10000 — радиус i-ой детали. Гарантируется что номера деталей уникальны.
Формат выходных данных:
В первой строке выведите через пробел M — количество деталей в самом мощном механизме и высоту стержня h. В следующих M строках выведите информацию о деталях от самой нижней детали на стержне до самой верхней. Каждая строка должна содержать три числа, разделенные пробелами: номер детали, ее высоту и ее радиус.
Если существует несколько вариантов собрать мощнейший механизм, выведите любой из планов сборки.
1 этап
Задача по математике 9 класс 1.1.3 (3 балла)
Локатор видит часть пространства, ограниченную конусом. Максимальный угол между образующими этого конуса равен 60 градусам. Объекты, находящиеся дальше расстояния a, уже далеко и не попадают в зону видимости локатора. Через ось конуса проведены две перпендикулярные плоскости, которые делят конус на четыре части. В одной из частей обнаружен объект в форме сферы, вписанный в эту часть. Сфера касается обеих перпендикулярных плоскостей, поверхности конуса и его основания. Длина образующей равна a. Найдите радиус этой сферы.
Задача по физике 9 класс 1.2.4 (3 балла)
В ходе эксперимента по выращиванию кристалла сломалась система охлаждения, и уже выращенный образец расплавился. Для изучения остался только график зависимости температуры от времени, но и он был поврежден. Восстановите цену делений на этом графике. Известно что теплопередача пропорциональна разнице температур, внешняя температура 400 K. Про материал известны: температура плавления 300 K, теплота плавления λ=24кКал/кг, теплоемкость жидкой фазы Сж=8000кал/кг*К, коэффициент теплопроводности 32 Дж/градус Масса образца 1 кг.

Запишите цену делений шкалы температуры. Ответ дайте в градусах, с точностью до целых.
Задача по физике 9 класс 1.2.5 (4 балла)
Спутник, находящийся на высоте H = 7000 км от центра планеты с массой M=1,076*1023 кг, переходит на точно такую же по высоте орбиту, пересекающую изначальную под углом α=5º. Найдите силу, с которой действовали маневровые двигатели спутника, если известно, что поворот занял t=30 с, а масса спутника m=50 кг. Ответ дайте в ньютонах с точностью до целых.
Задача по физике 10-11 класс 1.3.3 (2 балла)
Спутник массы m=100 кг, находящийся на орбите радиуса L=2500 км, обращаясь вокруг планеты массы M= 4,8017· 1022 кг, разгоняясь, совершает эллиптический переход на орбиту радиуса 2L=5000 км. Найдите время, требующееся на переход. Изменения скорости, производимые в апоцентре и перицентре, считать мгновенными. Ответ дайте в часах, с точностью до десятых.

Задача по физике 10-11 класс 1.3.5 (3 балла)
Ниже приведен график зависимости плотности атмосферы Юпитера от высоты.
Считая ускорение свободного падения g постоянным g=25м/с2, найдите глубину погружения, если зонд спускается с высоты H1=7∗ 104 км вниз без начальной скорости. Среднюю плотность зонда считайте равной ρ=1.49г/см3

Ответ дайте в километрах и округлите до тысяч.
Задача по информатике 1.4.3 «Полет» (6 баллов)
На высоте h метров над поверхностью планеты находится тело. В начальный момент времени его скорость равна v⃗метров в секунду. Вычислите время до момента касания телом поверхности планеты, если известно, что:
— h в начальный момент времени не превышает десяти километров, а мгновенная скорость — одного километра в секунду.
— На тело действует сила притяжения планеты. Ускорение, создаваемое этой силой, равно
 , и направлено к центру планеты. Здесь G — гравитационная постоянная, M — масса планеты, а R — расстояние от центра планеты до тела. Величину GM считайте равной 4× 1013, а радиус планеты — 6300000 метрам.
, и направлено к центру планеты. Здесь G — гравитационная постоянная, M — масса планеты, а R — расстояние от центра планеты до тела. Величину GM считайте равной 4× 1013, а радиус планеты — 6300000 метрам.— Так же на тело действует сила аэродинамического сопротивления. Можете считать, что ускорение, создаваемое этой силой, равно
 , где ρ — плотность
, где ρ — плотностьатмосферы на заданной высоте, выражаемая формулой
 — мгновенная скорость тела, а
— мгновенная скорость тела, а  — модуль мгновенной скорости.
— модуль мгновенной скорости.— При данных ограничениях смещение вдоль касательной к поверхности планеты много меньше ее радиуса планеты, поэтому кривизной планеты следует пренебречь.
Мы понимаем, что аналитически решить эту задачу сложно, поэтому примем ответ с абсолютной погрешностью 0.1 секунды. И предупреждаем, что слишком сильно менять состояние тела — не очень хорошая идея.
Формат входных данных:
В первой строке дано одно натуральное число h — высота тела в начальный момент времени, выраженная в метрах. Во второй строке даны два целых числа
 — координаты начальной скорости тела в метрах в секунду. Ось Oy при этом направлена в сторону, противоположную направлению силы гравитации, а ось Ox — перпендикулярна оси Oy.
— координаты начальной скорости тела в метрах в секунду. Ось Oy при этом направлена в сторону, противоположную направлению силы гравитации, а ось Ox — перпендикулярна оси Oy.Пример ввода 1:
100
10 10
Пример ввода 2:
1
0 0
Формат выходных данных:
Выведите единственное вещественное число — время до касания телом поверхности планеты, выраженное в секундах.
Пример вывода 1:
290
105.3283038851984
Пример вывода 2:
1.6649107662192795
2 этап
Задача 2.1 «Посадка на Луну» (макс. 180 баллов)

Луна — ближайший к Земле астрономический объект. Посадка корабля на Луну — это самое простое задание, с которым человечество справлялось уже не раз. Создание и запуск аппарата для исследования лунной поверхности состоит из нескольких этапов. В этой задаче мы мы рассмотрим только один, но самый интересный этап — посадку аппарата. Вам придется сконструировать собственный аппарат и составить техническое задание на его производство, дождаться результатов полета и получить телеметрию процесса посадки.
Успешно посадить аппарат с первой попытки не просто. В случае неудачи вам предстоит проанализировать данные телеметрии и изменить техническое задание для следующего запуска.
Постановка задачи
Это только первая, тренировочная задача, поэтому в ней есть несколько допущений: аппарат падает вертикально на поверхность Луны, его начальная скорость равна нулю, а из доступного оборудования есть только демпфер и тормозной двигатель.
Задача состоит в том, чтобы определить, в какой момент времени t1 нужно включить тормозной двигатель, чтобы к моменту посадки t1+t2 скорость корабля была бы меньше 50 м/с, иначе удар не удастся самортизировать с помощью демпфера.
Другими словами, вам нужно вычислить два параметра — время включения тормозного двигателя и время его выключения — и вставить их в программу полета аппарата.
Все исходные данные известны: это начальная высота, масса и радиус Луны, масса аппарата, сила тормозного двигателя.
Задача 2.2 «Посадка на Марс» (макс. 1650 баллов)
Красная Планета — намного более сложный объект для посадки космического аппарата, чем Луна. Во-первых, Марс намного массивнее, а значит сила тяжести играет куда большую роль. Во-вторых, на Марсе есть атмосфера, так что влияние сопротивления атмосферы на движение корабля около поверхности будет значительным.
В этой задаче также не будет рассматриваться работа аппарата на поверхности. В вашем распоряжении снова будет полностью сконструированный аппарат, но вам придется самостоятельно запрограммировать его полет: выбрать, в какой момент нужно будет включить тормозной двигатель, открыть парашют и т. д.
Анализ телеметрии позволит исправить ошибки, допущенные при посадке, уже в следующем аппарате.
Постановка задачи

По сравнению с Луной задача усложняется: теперь придется работать в двух измерениях. У аппарата есть начальная горизонтальная (орбитальная) скорость. К тому же, теперь на аппарат действует не только сила тяжести, но и сила аэродинамического сопротивления (Стокса), пропорциональная квадрату скорости аппарата. Однако, и в этой задаче есть упрощение: поверхность планеты принимается за плоскость. Также вам будет доступна специальная программа для расчетов.
Условие задачи делает аналитическое решение очень сложным, поэтому мы предлагаем вам качественно оценивать значения скоростей и сил, а также тщательно анализировать результаты неудачных полетов.
Задача 2.3. «Работа на поверхности Марса» (макс. 20000 баллов)
Конструирование аппарата
Мы предлагаем вам продолжить миссию по покорению Марса разработкой аппарата для работы на поверхности планеты. Совершив удачную посадку, ваш аппарат начнет передавать на Землю научные данные, которые позволят углубить знания человечества о Красной планете.
Условия победы:
За успешное решение этой миссии вы получаете победные баллы. В этой миссии вы получаете баллы за переданную на Землю научную информацию следующим образом: За каждый переданный на землю 1 Мегабит (1000 килобит) научной информации команда получает 0,1 балла (другими словами, количество баллов = переданная информация/1000). Вам дается 10 попыток. Каждая дополнительная попытка сверх этих десяти отнимает у команды 30 баллов. Таким образом можно получить не более 30 дополнительных попыток (т. е. Минус 900 баллов).В миссии также возможны следующие достижения:
- Исследователь — Передать научные данные с Марса любого объема (100 балл.)
- Первопроходец — Первыми по времени передать научные данные с Марса (200 балл.)
- Доставка оборудования — Самый тяжелый аппарат, севший на Марс и передавший данные (300 балл.)
- Экономичность — Самый легкий аппарат, севший на Марс и передавший данные (500 балл.)
- Космическая гонка — Передать научные данные с Марса в течение первых трех суток с момента получения задачи командой (300 балл.)
- Надежная конструкция — Аппарат проработал на Марсе все 72 часа (200 балл.)
Постановка задачи
Если с точки зрения физики задача остается прежней, то конструкторская ее часть будет заметно сложнее. Вам предстоит полностью сконструировать аппарат и составить программу не только посадки, но и планетарной активности. Аппарат может проработать на поверхности Марса не более 72 земных (!) часов.

Вам не придется конструировать произвольный аппарат с нуля. В вашем распоряжении будет аппарат сферической формы, его размер вы можете установить самостоятельно. Вам придется рассчитать требуемые внешние параметры аппарата (массу и радиус), выбрать необходимое для работы оборудование и научные приборы.
Мы рекомендуем следующий порядок разработки:
- сконструировать аппарат с максимальной полезной нагрузкой и посадить его;
- наполнить полезную нагрузку необходимым оборудованием для обеспечения максимальных научных результатов.
Помимо конструкции аппарата вам предстоит разработать программу полета, например, определить время, когда должны включаться и выключаться тормозные двигатели или научные приборы.
Задача 2.5 «Связь с Землей» (макс. 520)
КА движется по круговой орбите с заданной высотой в плоскости X0Y. Необходимо запрограммировать аппарат так, чтобы он передал на Землю заданное сообщение. При этом необходимо воспользоваться высокопроизводительной связью КА. Задача усложняется двумя факторами: сигнал экранируется Землей, антенна такой подсистемы имеет угол раскрыва (γ), заданный в параметрах КА.

Мы будем считать, что наземный измерительный пункт (НИП) отслеживает положение КА, поэтому потребуется только сориентировать аппарат на НИП.
В данной миссии вам не потребуется конструировать аппарат целиком, однако нужно будет подобрать несколько параметров конструкции аппарата — площади солнечных батарей и радиаторов, а также написать программу полета. Мы рекомендуем вам использовать наработки, полученные в предыдущей миссии.
КА оснащен подсистемой ориентации и стабилизации, которая позволяет задавать момент вращения посредством включения маховика, а также подсистемой высокопроизводительной связи, параметры которой указаны в таблице ниже. КА как и в первой тренировочной миссии в начале полета будет иметь стартовую угловую скорость, которую придется погасить для успешного выполнения миссии.

При конструировании аппарата вам необходимо рассчитать и указать площади для солнечных батарей и радиаторов на гранях 1-4 аппарата и площади радиаторов на гранях 5-6 аппарата, например:

Задача 2.7 «Съемка Земли из космоса» (макс. 12500 баллов)
Задача «Съемка Земли из космоса» посвящена съемке поверхности Земли из космоса малым космическим аппаратом. Вы должны будете сфотографировать объект на поверхности Земли и передать полученное изображение на наземный измерительный пункт (НИП), используя высокопроизводительную связь.

Задача 2.8. «SMS везде» (макс. 9200 баллов)
Задача «SMS везде» воссоздает работу спутника связи, который должен обеспечить прием и передачу сообщений между 18 наземными станциями (которые называются «0», «1», «2» и т.д.).

В вашем распоряжении будет 10 стартовых запусков. За каждый запуск после 10-го будет добавляться штраф в 150 баллов за запуск, и так до 20 дополнительных запусков (до -3000 баллов).
Постановка задачи
Каждое конструкторское бюро получает уникальный вариант, который содержит: стартовую высоту орбиты; список и названия наземных измерительных пунктов; таблицу сообщений для передачи (всего 5 сообщений).
КА должен последовательно доставить максимальное число сообщений, указанных в таблице. Как только аппарат получил сообщение от НИП, начинается отсчет времени доставки, которое не должно превысить допустимое время передачи.
На миссию дается 6 часов полета аппарата.
3 этап
Задача по математике 3.1.4 (4 балла)
Магнитометр выдает для каждого градуса долготы φ три координаты вектора магнитного поля (sin φ, sin 2φ, cos 2φ). Найдите долготу, на которой вектор магнитного поля имеет минимальную длину.
Задача по физике 3.2.2 (3 балла)

Космический корабль, покоящийся в открытом космосе, вдалеке от планет представляет из себя конструкцию, изображенную на рисунке. Корабль должен был выполнить маневр ускорения, включив на короткое время τ = 2c симметрично расположенные двигатели, однако, в результате технического сбоя сработал только один из них. Каков модуль скорости, которую приобрел после этого маневра корабль в системе отсчета, в которой исходно он покоился? На какой угол повернулся корабль на момент выключения двигателя относительно оси, перпендикулярной плоскости движения, проходящей через цент основного отсека корабля?
Параметры корабля: масса корабля M = 1200кг, расстояние между центрами отсеков L = 2м, тяга двигателя F = 710Н, мощность двигателя N = 50кВт. Момент инерции корабля относительно оси, проходящей через центр масс перпендикулярно штангам равен J = 903кг·м2. Центры шаров лежат на прямой, проходящей вдоль соединяющей их штанги. Массой штанг, уменьшением массы корабля в результате сгорания топлива и гравитационным взаимодействием можно пренебрегите. Считайте, что сила тяги не зависит от скорости, а масса в отсеках распределена однородно.
Задача по физике 3.3.3 (3 балла)

Спутник облетает Землю на геостационарной орбите высотой H = 35 786 км. У спутника есть одна солнечная батарея 2м х 10м направленная всегда перпендикулярно орбите спутника длинной стороной вдоль прямой соединяющей центры Земли и спутника (см. рисунок, плоскость батареи перпендикулярна плоскости рисунка). Коэффициент отражения света от батареи β = 75% (остальной свет батареей поглощается). На какое время нужно запустить двигатель гиродина с крутящим моментом 2 Н·м, чтобы скомпенсировать вращение спутника, полученное из за солнечного излучения за время движения от положения А до положения B по орбите? Солнечная постоянная L = 1367 Вт/м², радиус орбиты Земли RЗемли = 150 млн. километров. Считайте, что коэффициент отражения не зависит от угла падения света.
Гиродин — вращающееся инерциальное устройство, применяемое для высокоточной ориентации и стабилизации.
Задача по информатике 3.4.5 «Механизм» (3 балла)
Олимпиада это, конечно, здорово и интересно, но дома у Коли осталась компьютерная игра-головоломка. На новый уровень Коля перешел буквально перед самым отъездом из дома и теперь в уме размышляет, как будет проходить новый уровень. Задача заключается в следующем: Коля собирает какой-то заумный механизм. Для этого он должен последовательно устанавливать на стержень высоты h детали механизма.
Каждая деталь представляет собой диск некоторой высоты. Все детали задаются двумя параметрами: высота детали ki и радиус детали ri. Известно, что все детали, несмотря на то, что имеют разный вид, вносят равный вклад в мощность механизма. Коля же должен сделать самый мощный механизм из возможных. При сборке механизма действуют следующие правила Детали укладываются на стержень последовательно. Радиус детали, которая лежит выше, должен быть строго меньше радиуса любой детали, которая лежит ниже.
Суммарная высота всех деталей должна быть строго меньше высоты стержня.
Помогите Коле написать программу, которая сможет выдать план сборки самого мощного механизм.
Формат входных данных:
В первой строке задано число деталей 1≤N≤5000 и высота стержня h≤20000. В следующих N строках записаны тройки целых неотрицательных чисел idi — номер детали, 0≤ki≤1000 — высота i-ой детали и 1≤ri≤10000 — радиус i-ой детали. Гарантируется что номера деталей уникальны.
Формат выходных данных:
В первой строке выведите через пробел M — количество деталей в самом мощном механизме и высоту стержня h. В следующих M строках выведите информацию о деталях от самой нижней детали на стержне до самой верхней. Каждая строка должна содержать три числа, разделенные пробелами: номер детали, ее высоту и ее радиус.
Если существует несколько вариантов собрать мощнейший механизм, выведите любой из планов сборки.
Комментариев нет:
Отправить комментарий