Спросите Итана №78: почему E = mc2?

Самое знаменитое уравнение Эйнштейна вычисляется более красиво, чем это можно было бы ожидать.

Из специальной теории относительности вытекает, что масса и энергия являются разными проявлениями одного и того же – концепция, среднему уму незнакомая.
— Альберт Эйнштейн

https://geektimes.ru/post/279008/
Некоторые научные концепции настолько меняют мир и настолько глубоки, что практически каждый знает о них, даже если полностью и не понимает. Почему бы не поработать над этим вместе? Каждую неделю вы отправляете ваши вопросы и предложения, и на этой неделе я выбрал вопрос Марка Лиюва, который спрашивает:

Эйнштейн вывел уравнение E = mc². Но единицы энергии, массы, времени, длины уже были известны до Эйнштейна. Так как же оно так красиво получается? Почему там нет какой-нибудь константы для длины или времени? Почему это не E = amc², где a – какая-нибудь константа?

Если бы наша Вселенная не была устроена так, как сейчас, то всё могло бы быть по-другому. Давайте посмотрим, что я имею в виду.



С одной стороны, у нас имеются объекты с массой: от галактик, звёзд и планет до самых мелких молекул, атомов и фундаментальных частиц. Хотя они и крохотные, у каждой из компонент того, что известно нам под именем материи, имеется фундаментальное свойство массы, что означает, что даже если исключить его движение, даже если замедлить его до полной остановки, он всё равно будет оказывать влияние на все остальные объекты Вселенной.



Конкретно, он оказывает гравитационное притяжение на всё остальное во Вселенной, неважно, на каком расстоянии находится удалённый объект. Он притягивает всё к себе, испытывает притяжение ко всему остальному, а также обладает энергией, присущей самому его существованию.

Последнее утверждение контринтуитивно, поскольку об энергии, по крайней мере, в физике, говорят, как о возможности что-либо сделать – о возможности совершать работу. А что можно сделать, если ты просто сидишь на месте?

Перед тем, как ответить, давайте посмотрим на другую сторону монеты – вещи без массы.



С другой стороны, существуют вещи, не имеющие массы – например, свет. У этих частиц есть определённая энергия, и это легко понять, наблюдая их взаимодействие с другими вещами – при поглощении свет передаёт им свою энергию. Свет с достаточной энергией может разогревать материю, добавлять кинетическую энергию (и скорость), вышибать электроны на верхние энергетические уровни или вообще ионизировать, в зависимости от энергии.



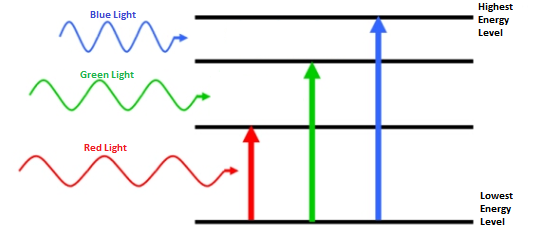
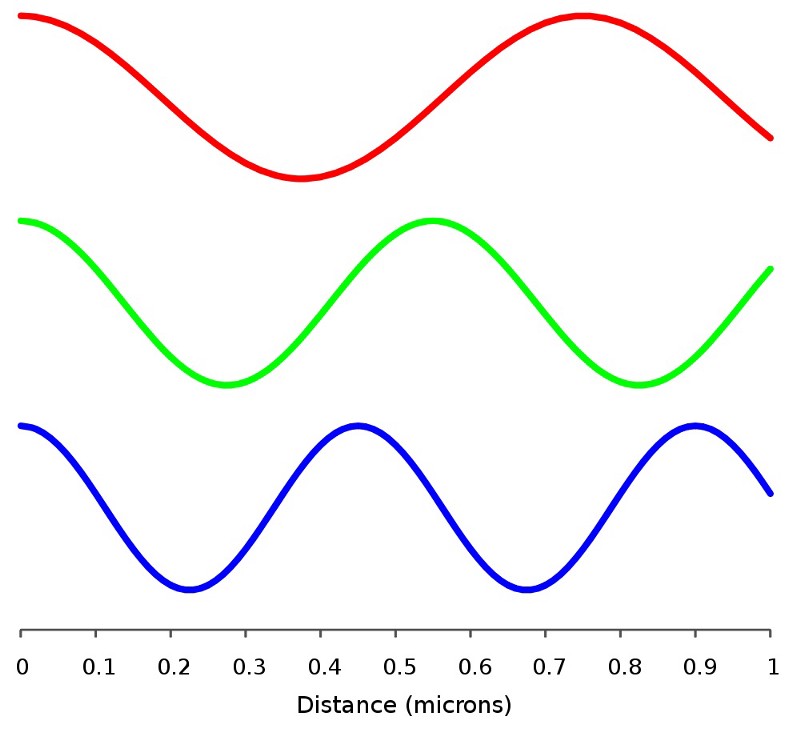
Более того, количество энергии, содержащейся в безмассовой частице, определяется только её частотой и длиной волны, произведение которых всегда равняется скорости движения частицы: скорости света. Значит, у более длинных волн частоты меньше, и энергия меньше, а у коротких – частоты и энергия выше. Массивную частицу можно замедлить, а попытки отобрать энергию у безмассовой приведут лишь к удлинению её волны, а не к изменению скорости.



Памятуя о вышесказанном, подумаем, как масса-энергия может быть эквивалентной работе? Да, можно взять частицу материи и частицу антиматерии (электрон и позитрон), столкнуть их и получить безмассовые частицы (два фотона). Но почему энергии двух фотонов равны массам электрона и позитрона, умноженным на квадрат скорости света? Почему там нет другого множителя, почему уравнение точно приравнивает E и mc²?



Что интересно, если верить СТО, уравнение просто обязано выглядеть, как E=mc², без всяких отклонений. Поговорим о причинах этого. Для начала представьте, что у вас есть коробочка в космосе. Она неподвижна, и с двух сторон у неё зеркала, а внутри находится фотон, летящий к одному из зеркал.



Изначально коробочка не двигается, но поскольку фотоны обладают энергией (и импульсом), когда фотон сталкивается с зеркалом с одной стороны коробки и отскакивает, коробка начнёт движение в том направлении, в котором изначально двигался фотон. Когда фотон достигнет другой стороны, он отразится от зеркала с другой стороны, изменяя импульс коробки обратно до нуля. И он продолжит отражаться таким образом, в то время как коробка половину времени будет двигаться в одну сторону, а другую половину – оставаться неподвижной.

В среднем коробка будет двигаться и, следовательно, так как у неё есть масса, будет иметь определённую кинетическую энергию, благодаря энергии фотона. Но важно также помнить про импульс, количество движения объекта. Импульс фотонов связан с их энергией и длиной волны очень просто: чем короче волна и выше энергия, тем выше импульс.



Подумаем о том, что это значит, и для этого проведём ещё один эксперимент. Представьте, что происходит, когда изначально двигается только сам фотон. У него будет определённое количество энергии и импульс. Оба свойства должны сохраняться, поэтому в начальный момент энергия фотона определена его длиной волны, а у коробки есть только энергия покоя – какая бы она ни была – и фотон обладает всем импульсом системы, а у коробки импульс нулевой.



Затем фотон сталкивается с коробкой и временно поглощается. Импульс и энергия должны сохраняться – это основные законы сохранения Вселенной. Если фотон поглощён, то существует только один способ сохранить импульс – коробка должна двигаться с определённой скоростью в том же направлении, в котором двигался фотон.

Пока всё нормально. Только теперь мы можем спросить себя, какова энергия коробки. Получается, что если мы идём от нашей обычной формулы о кинетической энергии, K_E = ½mv², мы предположительно знаем массу коробки, и, исходя из понятия импульса, её скорость. Но если мы сравним энергию коробки с энергией фотона, которой он обладал до столкновения, мы увидим, что у коробки энергии недостаточно.

Проблема? Нет, это довольно просто решить. Энергия системы коробка/фотон равна массе покоя коробки плюс кинетической энергии коробки плюс энергии фотона. Когда коробка поглощает фотон, большая часть его энергии переходит в увеличение массы коробки. Когда коробка поглотила фотон, её масса меняется (увеличивается) по сравнению с той, что была до столкновения.

Когда коробка вновь испускает фотон в другом направлении, она получает ещё больший импульс и скорость (что компенсируется отрицательным импульсом фотона в обратном направлении), ещё больше кинетической энергии (и у фотона есть энергия), но теряет взамен часть массы покоя. Если всё подсчитать (есть три различных способа это сделать, а тут ещё и описание), можно обнаружить, что единственное преобразование массы, позволяющее сохранить энергию и импульс, будет E = mc².



Если добавить любую константу, уравнение перестанет быть сбалансированным, и вы будете терять или приобретать энергию каждый раз при испускании или поглощении фотона. Обнаружив антиматерию в 1930-х, мы непосредственно увидели подтверждение того, что можно превратить энергию в массу и обратно, и результаты превращений точно совпадали с E = mc², но именно мысленные эксперименты позволили вывести эту формулу за несколько десятилетий до наблюдений. Только поставив фотону в соответствие эффективную массу, эквивалентную m = E/c², мы можем обеспечить сохранение энергии и импульса. И хотя мы говорим E = mc², Эйнштейн впервые записал формулу по-другому, присвоив энергетически эквивалентную массу безмассовым частицам.

Так что, спасибо за прекрасный вопрос, Марк, и надеюсь, что этот мысленный эксперимент поможет тебе понять, почему нам нужна не только эквивалентность массы и энергии, но и почему в этом уравнении есть только одно возможное значение для «константы», которое поможет сохранить энергию и импульс – а этого требует наша Вселенная. Единственное уравнение, которое работает, это E = mc². Присылайте мне ваши вопросы и предложения для следующих статей.