Эффект Оберта
Начнем пожалуй с Эффекта Оберта, хотя это крайне сложный эффект, но зато разобравшись с ним — мы поймем всю орбитальную физику. Для начала давайте зададимся вопросом — В чем сила, брат? — В лошадиных силах!Сколько лошадиных сил у ракетного двигателя?
Ответ странный — по разному, один и тот же килограмм топлива в одном и том же двигателе дает разное количество энергии. Причина в разной скорости на которой используется это топливо, чем больше скорость самой ракеты — тем больше энергии дает двигатель, причем этот же двигатель ускоряющий вбок (относительно текущей скорости) — будет давать меньше энергии, чем при ускорении вперед.
Давайте сразу рассмотрим 2 хороших и наглядных примера. Один из Ютуба от гаражного учёного Игоря Белецкого продемонстрировавшего эффект Оберта с помощью шприца, резинки и кое чего еще, а второй пример из Википедии.
Эксперимент кустарного производства.

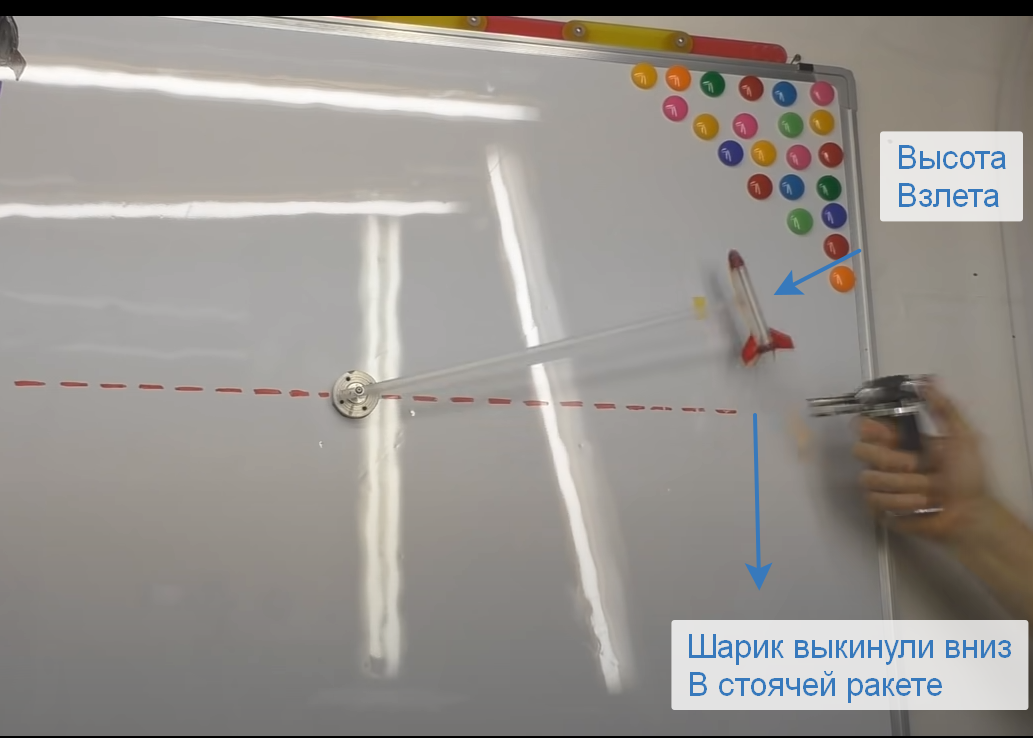
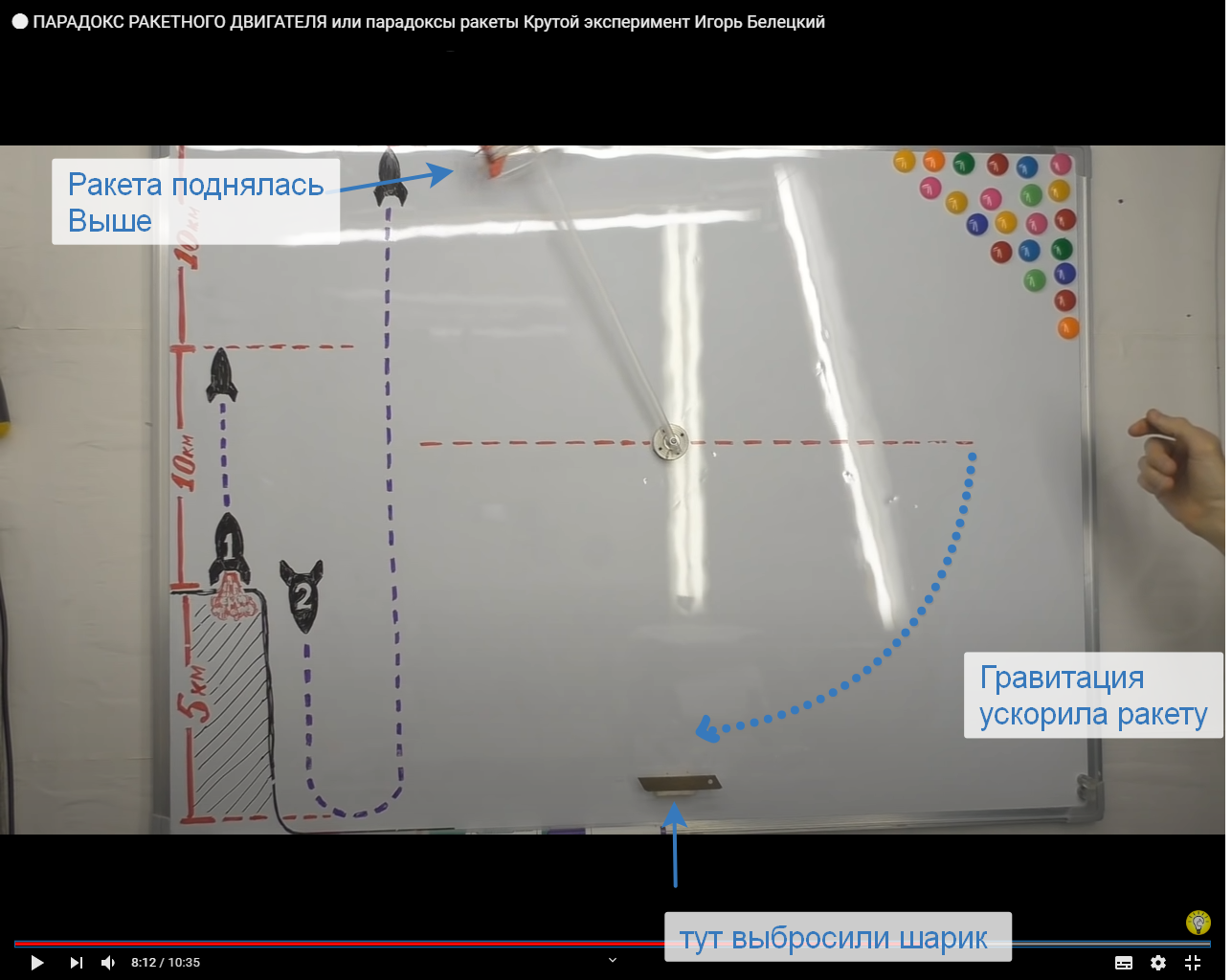
Источник: ютуб канал Игоря Белецкого
Из Википедии
Примечание для тех кто не читал про космические скорости
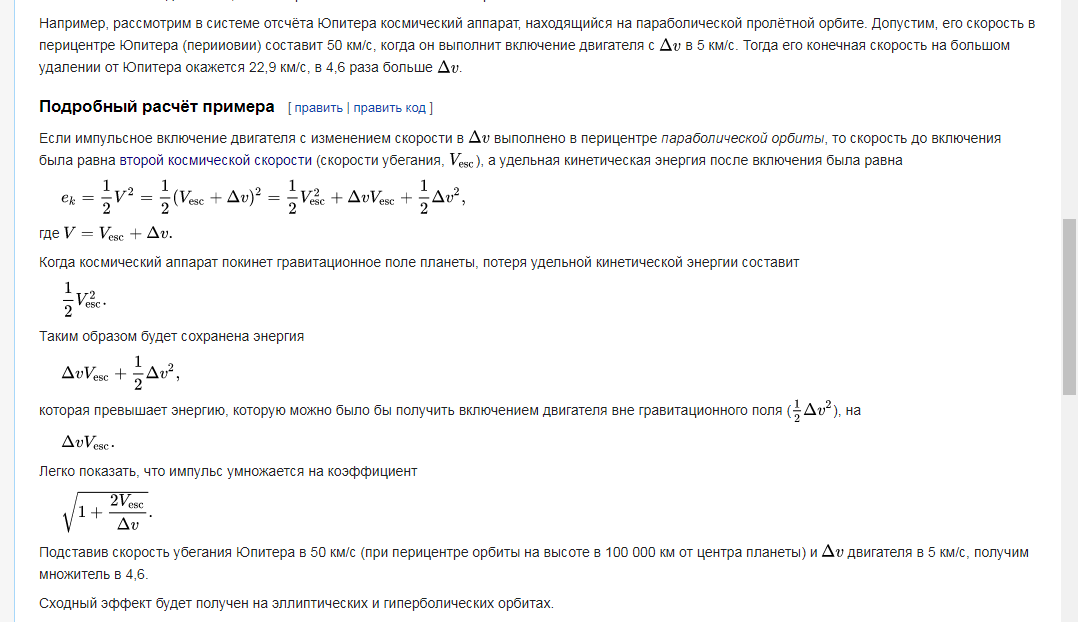
В ролике с ютуба — этот эффект можно даже увидеть своими глазами, чтобы понять почему так происходит, давайте рассмотрим кинетическую и «тепловую» энергию по отдельности.
Всё что нам надо знать о кинетической энергии в контексте орбитальной механики — это третий закон Ньютона: — Сила действия равна силе противодействия F= -F. Т.е. Если мы что то кидаем вперед со скоростью 10 м/с, то что то обязательно полетит в противоположную сторону с той же скоростью 10 м/с (при одинаковых массах).
И еще нам понадобится формула самой энергии E=mv22 (масса*скорость в квадрате/2), чтобы не заморачиваться с постоянным делением на 2, я буду всегда брать массу 2 кг. — тогда энергия будет равна просто скорость в квадрате. К примеру при скорости 10 м/с — энергия равна 10*10=100 Джоулей (за каждые 2 кг.).
Итак, давайте представим пушку на колесах которая катится и мы будем ускорять пушку выстрелами. Массу ядер возьмем 2 кг. Выстреливает она со скоростью +1 м/с (слабенькая конечно, зато считать удобно). Допустим пушка катится со скоростью 2 м/с и выстреливает в противоположную сторону — т. е.
Ядро в пушке до выстрела имело скорость 2 м/с и его энергия была 2 в квадрате = 4 джоуля, после выстрела его скорость стала 1 м/с и энергия 1 Дж. — т. е. После выстрела ядро потеряло 3 Дж, а пушка соответственно получила эту энергию. Массу и скорость пушки считать не будем, нам важно другое.
Теперь представим что пушка двигается 3 м/с, до выстрела ядро имеет энергию 3 в квадрате = 9 Дж, а после выстрела 2 в квадрате = 4 Дж, т. е. В этот раз ядро потеряло уже 5 джоулей и т.д, чем больше скорость пушки — тем больше энергии теряет ядро. Получается порох дает больше энергии? — Нет, прирост энергии от каждого выстрела увеличивается, но откуда берется начальная скорость пушки? Из тех же самых выстрелов, и чтобы у нас было 1 ядро на скорости 4 м/с — нужно выстрелить 5 ядер на меньшей скорости (цифра 5 с потолка, но смысл вы поняли) — т. е. Дополнительная энергия берется от предыдущих выстрелов. Теперь давайте разберемся как работает сам порох.
Как порох создает импульс

Хотя давайте не будем забирать у бедной Греты её детство, и возьмем православную католическую солнечную панель, зарядим аккумуляторы и будем рассматривать энергию в более понятном современному человеку виде. Электричество измеряют в Ваттах, а 1 Ватт = 1 Джоуль (у них разный физический смысл, но практический результат одинаковый = ускорение = чтобы ускорить 2кг. до 10м/с нужно 100 Ватт=100 Дж.)
Теперь берем сферическое колесо в вакууме с 2-мя грузами на краях, начинаем раскручивать электродвигателем и выкидываем грузы в разные стороны. Грузы как всегда 2 кг, само колесо нам не интересно и будем считать энергию затраченную только на раскручивание грузов. Раскрутим их до 10 м/с, для этого нам понадобится 10*10=100 Вт на каждый груз.

Тут всё просто, потратили 200 Ватт = получили 2 груза со скоростью 10 м/с в противоположные стороны. А теперь давайте добавим скорость самому колесу = 10 м/с.
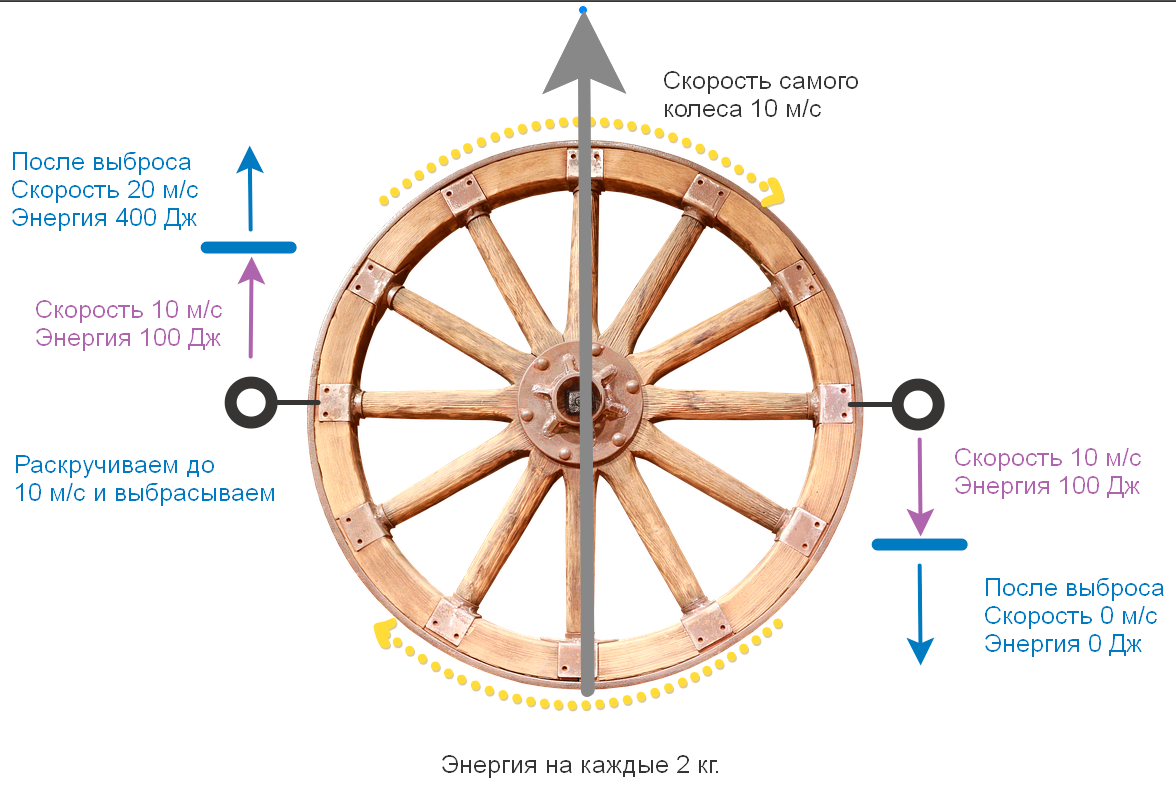
И тут мы видим интересную картину.
Для раскручивания мы также потратили 100 Дж на каждый груз = 200 Дж. +200 Дж. у каждого груза было изначально (они оба двигались вместе с колесом 10 м/с).
Ускорившийся груз увеличил свою скорость в 2 раза и вылетел со скоростью 20 м/с, а его энергия увеличилась в 4 раза — до 400 Дж. — по сути он забрал вообще всю энергию — и затраченную на раскручивание их обоих +200, и энергию груза который замедлился — еще +100 Дж. (+100 у него было изначально) — Закон сохранения импульса очень наглый закон — ускорившийся забирает всё. Вернее КПД при ускорении растет с 50% при нулевой скорости до 100% при скорости выброса равной скорости самого колеса.
Тоже самое происходит и в ракете которая сжигает/выбрасывает топливо со скоростью ~3 000 м/с и при ускорении КПД двигателя растет, но для выхода на круговую орбиту нужна скорость минимум 7 900 м/с и давайте посмотрим что будет если скорость самого колеса будет больше скорости выброса.
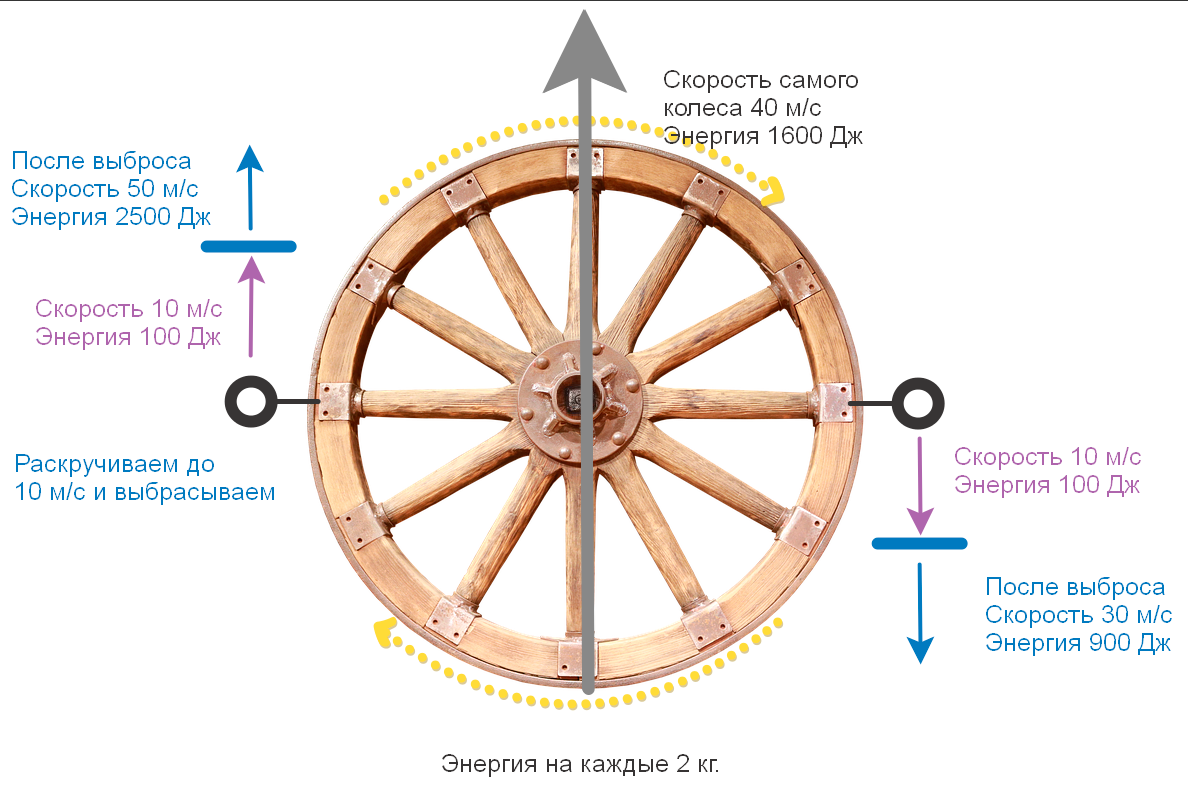
Тут мы опять потратили 200 Дж, а ускорившийся увеличил свою энергию с 1600 до 2500 = он получил 900 Дж = и он опять забрал всю энергию затраченную на раскручивание 200 Дж и +700 Дж, которые потерял груз вылетевший назад (1600-900=700). Иногда говорят, что КПД ракетного двигателя становится больше 100%, но нужно понимать, что здесь работают сразу 2 закона сохранения (закон сохранения энергии и закон сохранения импульса). Мы будем рассматривать их в рамках классической физики — в которой импульс — это свойство пространства (если мы кинем камень в вакууме и без гравитации со скоростью 10 м/с — то он никогда не остановится и всегда будет лететь со скоростью 10 м/с — потому что пространство такое — ровное, симметричное и без трения) — импульс описывается тремя законами Ньютона.
А энергия это …. хрен знает что, но она описывается тремя законами термодинамики, с ней без энтропии и кота Шрёдингера не разобраться — к счастью в орбитальной механике мы можем обойтись и без понимания откуда берется энергия — мы будем рассматривать её как свойство материи — «бензин горит потому что он бензин», а у любого ракетного двигателя есть такой параметр: Удельный импульс.
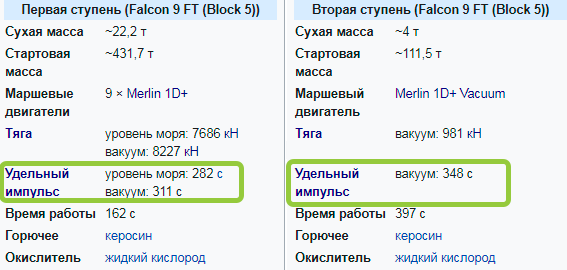
Умножаем это число на 10 и получаем скорость вылета топлива из сопла — для второй ступени Falcon 9 это 348*10=3 480 м/с, из этого параметра мы можем понять всё что нам надо. И довольствоваться мы будем относительностью Лапласа — не важно на какой скорости мы выкидываем массу — в примере с колесом и 2-мя телами, грузы всегда вылетают с одной и той же скоростью +-10 м/с относительно самого колеса, а в контексте ракеты это означает, что если 1 кг топлива может разогнать ракету с 0 до 10 м/с, то этот же килограмм топлива может ускорить ракету и с 10 000 до 10 010 м/с, несмотря на то, что во втором случае ракета получит в тысячу раз больше энергии — это и называется эффект Оберта.
Теперь давайте вернемся к самому первому примеру с гаражной ракетой. Там на скорости — КПД «двигателя» шарика был выше, но прежде всего дело в гравитации — чтобы поднять шарик на высоту — нужно затратить энергию, а при падении она возвращается, и если бы мы измерили скорость удара шарика об пол, то в первом случае шарик упал с большей высоты и ударился сильнее, а во втором с меньшей высоты и ударился слабее — он отдал больше энергии, потому что у него и было больше энергии изначально — её он получил от экспериментатора поднявшего его на высоту и на Земле из эффекта Оберта получить «прибыль» нереально.
Но с Юпитером ситуация другая. Про гравитацию и космические скорости я подробно писал в прошлой статье, здесь будет очень коротко. Дело в том, что гравитация даёт/забирает не скорость (км/с), а энергию (Джоули). И в случае с Юпитером, мы начали на него «падать» с околонулевой скоростью и при максимальном сближении мы ускорились до 50 км/с (мы получили от него 2 500 МДж энергии на каждые 2 кг), мы включили двигатели и ускорились до 55 км/с и наша энергия стала 55*55=3025 МДж, а когда мы вылетели «за границу» его гравитации — он забрал обратно не скорость (50 км/с), а энергию которую он нам дал (2500 МДж) итого у нас осталось 3025-2500=525 МДж, чтобы получить скорость из энергии извлекаем квадратный корень = 22,9 км/с. Тут мы получили именно «прибыль», потому что мы не взлетали с Юпитера и у нас никогда не было скорости 50 км/с. Гравитацию очень удобно представлять как яму.

И в случае с Юпитером, мы как бы «вытащили» топливо с глубины условно 10 тысяч километров (с Земли), а сбросили на «глубине» 200 тысяч километров и мы вылетели из ямы, а большая часть топлива так и осталась в глубине этой ямы (на орбите Юпитера), хотя мы могли точно также подойти ближе к Солнцу и эффект был бы еще больше — чем ближе к массивному телу — тем больше «глубина». Поэтому при межпланетных перелетах эффект Оберта действительно может давать «прибыль» и его используют всегда, но до вылета с Земли — вся дополнительная энергия берется от сжигания предыдущих тонн топлива.
Формула Циолковского
Поскольку топливо всегда вылетает с одинаковой скоростью=ракета получает одинаковое ускорение, запас «скорости» у ракеты можно измерить в км/с (характеристическая скорость), например характеристическая скорость 10 км/с означает, что ракета может ускориться с 0 до 10 км/с, или сначала ускориться на 6, потом затормозить на 1, и опять ускориться на 3 (в сумме 10). А масса топлива напрямую зависит от скорости вылета топлива из сопла (удельный импульс) и тут то и возникает проклятье Циолковского.V=I∗ln(m1m2)
V-Конечная скорость ракеты
I-Удельный импульс
M1- Начальная масса ракеты с топливом
M2- Конечная масса ракеты без топлива
Если мы возьмем ракету массой 271 кг полностью состоящую из топлива и с удельным импульсом 3 км/с, то при ускорении с 0 до 3 км/с масса топлива уменьшится в 2,71 раза (число e) и у нас останется 271/2,71=100 кг топлива, при ускорении еще на 3 км/с, до 6 км/с произойдет опять тоже самое и у нас останется опять в 2,71 раза меньше топлива 100/2,71=37 кг, и так далее. Поскольку конструкция ракеты не весит 0 (обычно массу конструкции берут 10%) тогда мы можем смело брать модификатор 3. Пример оставлю под спойлером.
Слабонервным не смотреть!!!
Хотя мы очень много чего упростили, но число получилось очень близкое к действительности (в идеале нужно как раз ~18 км/с), а ракета Сатурн 5 возившая говорящих обезьян на Луну имела стартовую массу 3 000 тонн, а с Луны вернулось всего 5 тонн = в 600 раз меньше. И эта ракета была размером с 30-ти этажный дом (110 м). По сути разогнаться более чем в 6 раз быстрее удельного импульса практически невозможно. Хотя уже лет 50 обещают ядерный двигатель с удельным импульсом 8 000 м/с и с таким двигателем полет до Луны и обратно потребовал бы всего 8 кг. топлива, но пока этот двигатель так и остается по ту сторону телевизора. Хотя на самом деле всё ещё ужасней, двигатели с высоким УИ ускоряют очень долго и часто даже не могут преодолеть ускорение свободного падения на Земле, и для старта с поверхности они не годятся, а самые ужасы как раз происходят при старте.
Чтобы подняться на высоту Луны, нужна скорость старта ~11 км/с, а главный недостаток ракет в том, что они не ускоряются мгновенно. И хотя эффект Оберта не дает прибыли на Земле, его вообще можно лишиться, потому что у ракеты помимо удельного импульса, есть такой важный параметр для старта: Тяга.

Делим кило Ньютоны на тонны 7680/549=~14 м/с, и получаем ускорение ракеты за секунду, а на поверхности Земли ускорение свободного падения ~10 м/сс2, и если бы двигатель работал 10 секунд в вакууме — мы бы ускорились на 140 м/с (без учета уменьшения массы ракеты), но из-за гравитации мы ускорились всего на 40 м/с, а от текущей скорости у нас зависит КПД двигателя, и как в случае с гаражной ракетой, когда она получила больше энергии от шарика на меньшей высоте, у взлетающей ракеты происходит противоположный процесс, и чем быстрее ракета набирает высоту — тем быстрее кинетическая энергия переходит в потенциальную и тем меньше энергии дает топливо, вернее КПД двигателя всё равно растет, но не так быстро как мог бы, если бы мы ускорялись с минимальным набором высоты. Поэтому, чем больше ракета наклонена к горизонту, тем медленнее растет высота и мы получаем больше от эффекта Оберта. Но тогда мы дольше тремся об атмосферу. Хотя атмосфера создаёт во много раз меньше потерь, по сравнению с выгодой которую мы упускаем — трение создает температуру и нам понадобится более тяжелая термозащита, которую в конечном итоге придется вытаскивать на орбиту. Но и это еще не всё, через ~2 минуты сгорает ~ 75% топлива и масса уменьшается почти в 4 раза, а двигатель то у нас тот же самый и он как сжигал по ~2,5 тонны в секунду — так и сжигает, только вначале он толкал ~600 тонн с ускорением 14 м/сс2, а теперь он толкает 150 тонн с ускорением 14*4=56 м/сс2 = перегрузки увеличиваются в 4 раза. Мы конечно можем уменьшить подачу топлива, но тогда вырастут гравитационные потери (это последние секунды перед отделением первой ступени). В конечном итоге всё это приводит к тому, что мы теряем около половины топлива на эти так называемые гравитационные потери (хотя это скорее упущенная выгода).
Поскольку топливо нужно выбросить (сжечь) на минимальной высоте с минимальным ускорением вверх, сначала ракеты разгоняют до первой космической скорости (~7,9 км/с для Земли) и выводят на самую низкую круговую орбиту (НОО 180-200 км) и совершенно не важно куда вы летите на Луну/Марс или ГСО, сначала надо перейти к круговому движению и перестать «спорить» с гравитацией.
Фух, пройдя через все эти перегрузки, гравитационные потери, огненную атмосферу и другие околоземные ужасы — мы оказываемся на низкой опорной орбите (НОО ~180 км). Допустим нам надо на геостационарную орбиту (на высоту ~35 000 км). Самую дебильную траекторию перехода между орбитами вы наверняка много раз видели в голливудских блокбастерах — когда ракету поворачивают вертикально и включают двигатели против гравитации. На самой низкой орбите до земли всего 200 км — в 3 раза меньше чем от Москвы до Питера!!!.. Ускорение свободного падения на такой высоте меньше всего на 5%, и составляет ~9,2 м/с за секунду. Мы постоянно падаем вниз, но из-за скорости 7,9 км/с вперед, круглая земля постоянно «уходит из под ног», поэтому мы хоть и постоянно падаем, но наша высота не меняется. И к счастью, находясь на круглой орбите мы можем ускоряться только вперед и нам не будет мешать гравитация…
Но есть еще один вариант, менее дебильный по сравнению с ускорением вверх, но не менее дебильный вообще. Давайте его тоже рассмотрим, так, чисто поржать.
Мы двигаемся вперед, ускоряться вверх, нам будет мешать гравитация, но ведь у нас 3 измерения!!! Мы же можем ускоряться вбок. Что произойдет?
Для удобства давайте возьмем скорость ракеты 8 км/с и скорость вылета топлива тоже 8 км/с и посмотрим какая скорость будет у топлива после вылета.
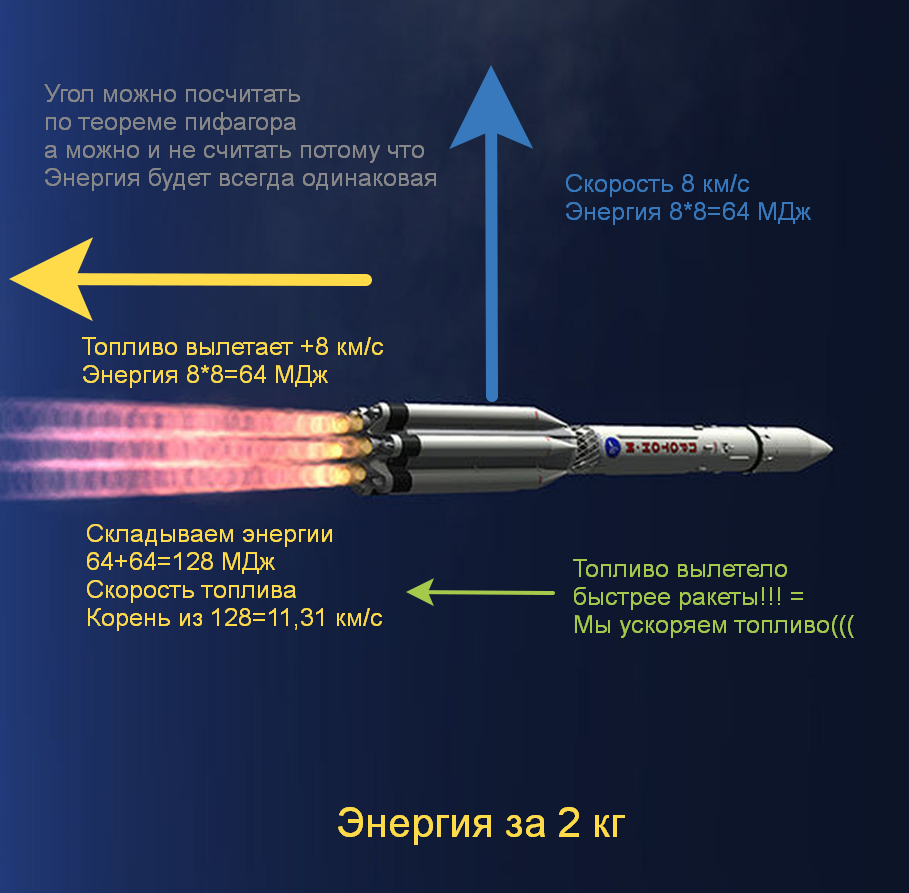
Итак изначально топливо двигалось 8 км/с (64 МДж) вперед вместе с ракетой, потом вылетело +8 км/с (+64 МДж) влево относительно ракеты, и мы можем посчитать угол (45 градусов) и сказать что топливо двигается 11,31 км/с относительно картинки и его энергия 128 МДж, а можем и не считать угол и сказать что топливо двигается 8 км/с влево (64 МДж) и одновременно 8 км/с вверх (64 МДж), а энергии у него всё равно 128 МДж. т. е. Топливо в любом случае ускорилось, а мы же вроде собирались ускорить ракету… Господи, что с ракетой!? Неужели она замедлилась и вот вот упадет на Землю?
Не переживайте, с ракетой всё хорошо — она тоже ускорилась, и ускорилась она на те же 64 МДж, чтобы посчитать угол и скорость, нужно знать разницу масс, но нам важно другое. По сути у нас получилось тоже самое что было в первом примере с колесом, когда оно не двигалось и у нас 2 груза ускорились в противоположные стороны получив одинаковую энергию, и КПД тогда был 50% — сюрприз — эффект Оберта зависит не только от скорости, но еще и от направления и перестает работать при любом отклонении от текущего вектора скорости. В этом примере мы получили в 3 раза меньше энергии, чем если бы выбрасывали топливо назад, и это при ядерном импульсе 8 км/с (при 3 км/с ~ в 6 раз меньше) — это называют потери на манёврах и на самом деле, после выхода на орбиту — повернуть влево/вправо практически невозможно и поэтому ракеты ускоряются только вперед, а если при выходе на орбиту промахнуться хотя бы на 30 градусов, то дешевле запустить новую ракету, чем менять вектор скорости у этой. К счастью в эпоху GPS и компьютеров, ракеты выходят на орбиту с очень высокой точностью, и потери на манёврах околонулевые.
Как подняться с высоты 200 км на высоту 35000 км?
Учитывая всё вышеописанное, единственное направление ускорения ракеты — вперед и перпендикулярно гравитации.

При ускорении перпендикулярно гравитации — высота растет с противоположной стороны планеты (гравитирующего тела) и чтобы перелететь с Низкой опорной орбиты (~200 км + скорость ~8 км/с) на Геостационарную орбиту (~35 000 км + скорость ~3 км/с), нам нужно ускориться до ~10,4 км/с (8+2,4), наша круговая орбита станет эллиптической и на противоположной стороне мы поднимемся на высоту 35 000 км, а наша скорость будет 1,7 км/с (при отдалении гравитация забирает энергию). В этой точке мы будем опять двигаться перпендикулярно гравитации и нам нужно ускориться до ~3 км/с, чтобы опять увеличить высоту с противоположной стороны и сделать нашу орбиту идеально круглой — Это называется Гомановский перелёт и это самый дешевый способ перелета в космосе — мы всегда ускоряемся только вперед и нам никогда не мешает гравитация.
По этой же траектории делаются перелёты и между планетами и как вы уже догадались, хотя минимальное расстояние от Земли до Марса ~55 миллионов километров — это почти ни на что не влияет, потому что прилетим мы на Марс с противоположной стороны Солнца пройдя около 400 млн. км — поэтому перелет и длится около 8 месяцев.
Сократить время перелета крайне сложно, вернее быстро вылететь с Земли то легко и при стартовой скорости ~16,5 км/с мы долетим до Марса за 3 месяца, но вот при подлете к нему у нас не совпадут вектора скорости. Упрощённо говоря — мы будем двигаться 1 км/с и Марс 1 км/с, но при этом мы будем лететь вперёд, а Марс влево и нам потребуется гигантский тормозной импульс. А если говорить точнее, то разница скоростей будет 21 км/с, + еще нам надо 16,5 км/с для старта с Земли = 37,5 км/с = массу ракеты считайте сами.
Неужели всё пропало и мы никогда не колонизируем Марс?
Если Ваш дедушка был зажиточным Рептилоидом и оставил Вам в наследство пару тонн антиматерии, то вы конечно можете лететь на Марс по любой траектории с любой скоростью (хоть каждые выходные). Но практика показывает, что на Землю прилетают в основном нищие Рептилоиды у которых нет денег даже на собственную летающюю тарелку — Вы видели хоть одну парковку НЛО? — вот вот — потому что Рептилоиды прилетают на такси.
Поэтому для нас остается лишь бюджетный Гомановский перелёт. Но не спешите отчаиваться — орбитальная механика очень парадоксальна. Как вы думаете, почему после полета человеков на Луну, за 50 лет на Марс отправили 4 Марсохода, а Луноход отправили всего 1 (и то Китайский)?
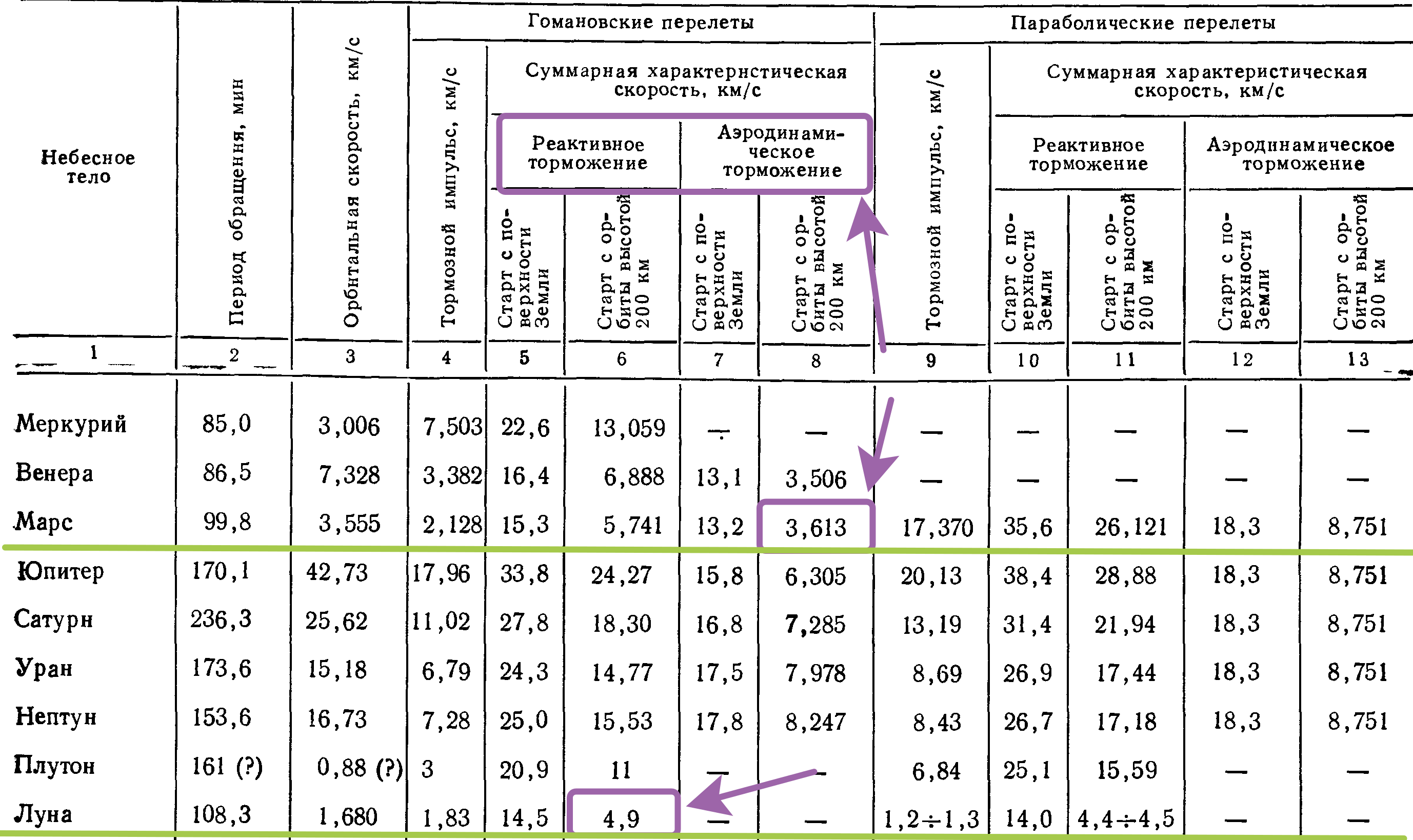
Таблица: Левантовский В.И. Механика космического полета в элементарном изложении.
Примечание: Расчеты Левантовского с учетом потерь.
А всё потому, что чтобы долететь до Луны нужна стартовая скорость 11,1 км/с (я потери не учитываю — это идеальный расход), а чтобы отправиться на Марс нужна стартовая скорость 11,5 км/с, всего на 0,4 км/с больше, но при этом, на Луне придется тормозить двигателями (1,83 км/с для выхода на орбиту Луны и + 1,68 км/с для посадки на поверхность Луны = 3,51 км/с), а на Марсе для торможения можно использовать атмосферу. И по сути вывести спутник на Марсианскую орбиту дешевле чем на Лунную!!! Я вам даже больше скажу, чтобы вывести спутник на ГСО нам надо импульс 10,4 км/с + потом еще 1,3 = 11,7 км/с, а на Марс 11,5 км/с (хотя нужно учитывать что термозащита не весит 0).
К Человекам это конечно не относится, потому что за 260 дней полета на Марс — Люди сожрут больше чем ракета, но с точки зрения грузов — это крайне удивительно — отправить трактор на орбиту Марса, дешевле чем на орбиту Луны.
Полностью посадить трактор на поверхность Марса вряд ли получится (атмосфера слишком «пустая»), но тем не менее львиную часть скорости также можно погасить с её помощью и посадка грузов на Марс, тоже дешевле чем на Луну (или по крайней мере сопоставима). Атмосфера даёт удивительные возможности.
Вернуться с Марса конечно же намного дороже чем с Луны. Хотя если немного помечтать и представить что мы можем полностью затормозить об атмосферу, то нам надо 11,5 км/с туда и 5,7 км/с обратно = 17,2 км/с, а для Луны 11,1 туда + 3,51*2 (посадка/взлет)=18,12 км/с — на ~0,9 км/с больше))). Но гравитационные потери при старте с Марса будут больше чем с Луны, да и термозащита нужна, поэтому в реальности получится в 3-5 раз дороже (по массе топлива) для грузов, а для обезьян так даже представить страшно.
Опять же — это если мы тащим топливо для возврата с Земли. Если же мы производим топливо в месте посадки, то ситуация сильно меняется и для вылета с Луны на Землю нам нужно 3,51 км/с (с Марса 5,7) — Лунная горючка дешевле Марсианской, но на Марсе дешевле посадка и нам проще построить само производство, а проклятье Циолковского очень страшная штука и даже сэкономив 1 км/с на посадке — мы сможем отправить в 1,5 раза больше полезной нагрузки.
Удивительно, но у колонизации Марса даже есть преимущества перед Луной. Да и саму Луну колонизировать с Марса проще, чем с Земли. Земля-Луна 11,1 км/с, а Марс-Луна 5,7 км/с. И если бы на Марсе тоже была жизнь — они бы уже давно колонизировали нашу Луну.
Орбитальная механика парадоксальна — гравитация создаёт «рельеф» и Солнечная система на самом деле не такая как можно увидеть в телескопе. В следующей статье мы рассмотрим этот «рельеф» подробней и постараемся найти ответ на вопрос — где самая дешевая горючка в Солнечной системе. А чтобы понять этот «рельеф» нам понадобится только формула Циолковского и Вторая космическая скорость (обязательно прочитайте прошлую статью про космические скорости). И всё на максимально простых примерах.
Те кто читал прошлую статью, знают, что у меня есть знакомый Рептилоид, и вот после пятой новогодней рюмки он мне такого нарассказывал! Он говорит, что у них есть технология с помощью которой они меняют орбиты целых планет. Сначала они берут «Юпитер» и какой-нибудь небольшой «Плутон», спускают их орбиты ближе к «Солнцу», но «Плутон» поворачивают в противоположную сторону и сталкивают лоб в лоб с «Юпитером» на скорости 600 км/с каждый и хотя «Юпитер» в 20 000 раз тяжелее «Плутона», но из-за огромной скорости столкновения он нагревается до нескольких тысяч градусов и начинает светить как лампочка. И потом они выкидывают эту «лампочку» из своей звездной системы в другую со скоростью 200-300 км/с. Да, перелёт длится долго — несколько тысяч лет, зато они перемещаются с комфортом — с мини «Солнцем» (остывает очень долго). Потом они прилетают к нужной звезде, разворачивают свою группировку летающих тарелок и выкидывают все планеты обратно к своей родной звезде. И они так насобирали уже несколько тысяч планет — им уже парковать их негде. Они уже даже слепили 80 «Юпитеров» в 1 и зажгли второе «Солнце».
Как летают эти тарелки он мне еще не рассказал, но рассказал уже много чего другого, так что обязательно подписывайтесь на канал — дальше будут технологии НЛО.
Ну и обязательно сделайте репост, или неужели вам нравится то, что происходит с интернетом? Когда заходишь в тренды ютуба — а там в топе видео как Влад бумага купается в … чипсах. Неужели вы не понимаете почему так происходит? — а всё потому, что школьники делают репосты — а вы нет!!! Как говорил Конфуций в своем письме Аристотелю: — Кто не хочет сам делать репосты — будет читать то, что репостят школьники!

Комментариев нет:
Отправить комментарий