Важное уточнение — калькулятор обычный, без кнопки sin. Как в бухгалтерии или на рынке.
Под катом три разных варианта решения из разных эпох, от древнего Самарканда до США времён холодной войны.
Первое, что приходит в голову — вот такое заклинание:
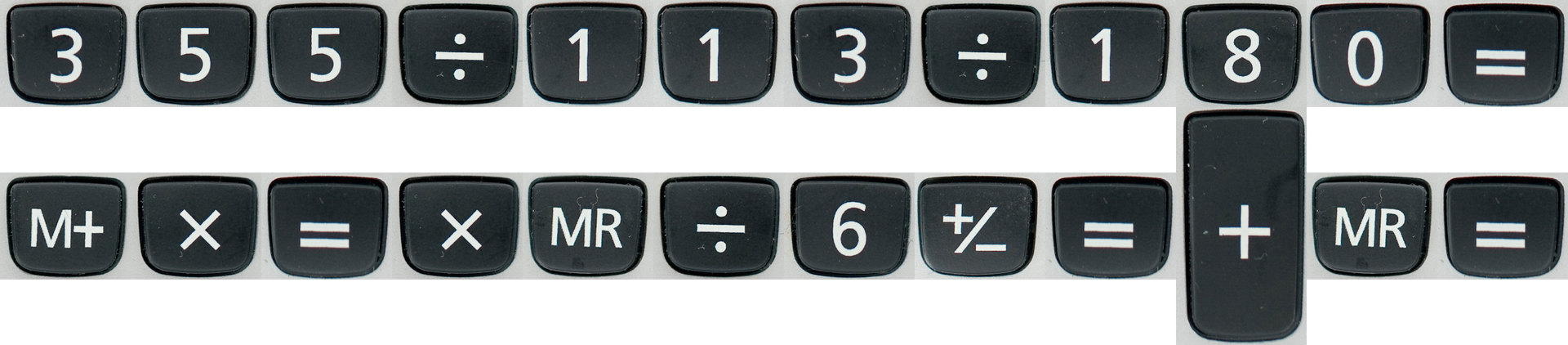
http://habrahabr.ru/post/271889/
Переведём эту путаную партитуру для калькулятора на более понятный язык bc. Он часто используется как калькулятор в командной строке UNIX-подобных операционных систем. Увидим примерно следующее:
Описанный выше общеизвестный трюк появился только в 1715 году. Тем не менее значения тригонометрических функций были известны намного раньше, и с заметно большей точностью.
Заведующий Самаркандской обсерваторией Гияс-ад-дин Джамшид ибн Масуд аль-Каши (غیاث الدین جمشید کاشانی) составил таблицы тригонометрических функций с точностью до 16-го знака ещё до 1429 года. В переводе с персидского на bc его заклинание применительно к нашей задаче выглядело примерно так:
Обратите внимание на то, что мы по-прежнему используем только сложение, вычитание, умножение, деление и квадратный корень. При желании все эти операции можно выполнить вообще на бумажке в столбик. Cчитать квадратный корень в столбик раньше даже учили в школе. Это занудно, но не очень сложно.
У пытливого читателя может возникнуть законный вопрос: как же считает значение синуса калькулятор, у которого есть такая кнопка?
Оказывается, что большинство калькуляторов используют совершенно третий способ — «цифра за цифрой», родившийся в недрах военно-промышленного комплекса США во время холодной войны.
Под катом три разных варианта решения из разных эпох, от древнего Самарканда до США времён холодной войны.
Простое решение
Первое, что приходит в голову — вот такое заклинание:
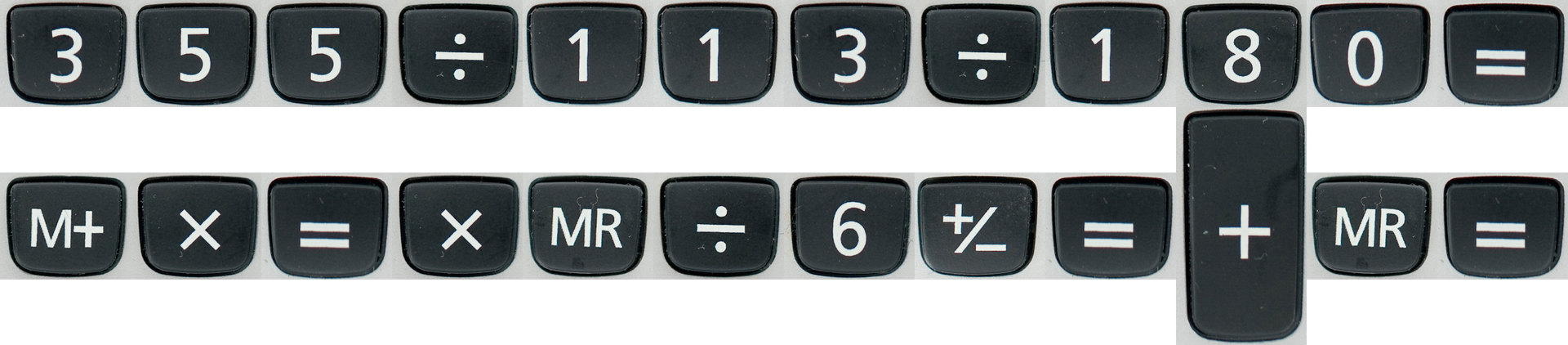
http://habrahabr.ru/post/271889/
Переведём эту путаную партитуру для калькулятора на более понятный язык bc. Он часто используется как калькулятор в командной строке UNIX-подобных операционных систем. Увидим примерно следующее:
Интересное решение
Описанный выше общеизвестный трюк появился только в 1715 году. Тем не менее значения тригонометрических функций были известны намного раньше, и с заметно большей точностью.
Заведующий Самаркандской обсерваторией Гияс-ад-дин Джамшид ибн Масуд аль-Каши (غیاث الدین جمشید کاشانی) составил таблицы тригонометрических функций с точностью до 16-го знака ещё до 1429 года. В переводе с персидского на bc его заклинание применительно к нашей задаче выглядело примерно так:
Обратите внимание на то, что мы по-прежнему используем только сложение, вычитание, умножение, деление и квадратный корень. При желании все эти операции можно выполнить вообще на бумажке в столбик. Cчитать квадратный корень в столбик раньше даже учили в школе. Это занудно, но не очень сложно.
Как считает сам калькулятор
У пытливого читателя может возникнуть законный вопрос: как же считает значение синуса калькулятор, у которого есть такая кнопка?
Оказывается, что большинство калькуляторов используют совершенно третий способ — «цифра за цифрой», родившийся в недрах военно-промышленного комплекса США во время холодной войны.
Комментариев нет:
Отправить комментарий